bonjour à tous, voici un exo que notre prof de crypto nous a balancé en disant qu'on est trop "cancre" :hum: pour le résoudre, or même si je ne peux pas y arriver seul je veux quand même le comprendre pour ne plus subir un affront pareil :briques:
Je vous remercie à tous pour vote aide ^^
Exo:
Pour n = pq avec p et q deux nombres premiers impaires distincts on pose:
lambda(n) = [ (p-1) (q-1) ] / pgcd (p-1, q-1)
Supposons que l'on modifie RSA en imposant ab congrue à 1 mod lambda(n). Montrer que c'est encore un système de chiffrement.
2. Si on prend p = 37 et q = 79 et b = 7, calculer a dans les deux cas.
encore merci pour votre aide ^^ :we:
Exo cryptologie
6 messages
- Page 1 sur 1
Bonjour,
il suffit de reprendre la démonstration pour le RSA classique :
(q-1)}{\alpha_n}) avec
avec 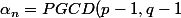) . Si M est le message et
. Si M est le message et 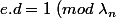) ou encore
ou encore 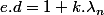 alors :
alors :
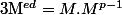^{\frac{k(q-1)}{\alpha_n}}=M\;(mod\; p)) si
si =1) (petit théorème de Fermat) sinon
(petit théorème de Fermat) sinon 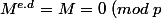) donc dans tous les cas
donc dans tous les cas  est divisible par
est divisible par  .
.
De la même manière est divisible par
est divisible par  et puisque
et puisque  et
et  sont premiers entre eux
sont premiers entre eux  est divisible par
est divisible par  (lemme d'Euclide) autrement dit
(lemme d'Euclide) autrement dit 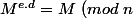)
il suffit de reprendre la démonstration pour le RSA classique :
De la même manière
Eh bien les deux cas sont :
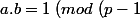(q-1))) et
et
(q-1)}{pgcd(p-1;q-1)}\))
on a :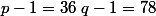 et
et =6) donc
donc (q-1)=2808) et
et (q-1)}{pgcd(p-1;q-1)}=468) .
.
Tu dois donc trouver l'inverse de modulo 2808 et aussi trouver l'inverse de
modulo 2808 et aussi trouver l'inverse de  modulo 468, pour cela tu peux utiliser l'algorithme d'Euclide étendu.
modulo 468, pour cela tu peux utiliser l'algorithme d'Euclide étendu.
on a :
Tu dois donc trouver l'inverse de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
