Exo calcul de norme.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
shar
- Membre Naturel
- Messages: 75
- Enregistré le: 28 Aoû 2017, 21:12
-
 par shar » 21 Jan 2018, 20:26
par shar » 21 Jan 2018, 20:26
Bonsoir,
voilà l'énoncé qui me pose soucis,
"Soit
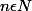
, on munit

de son produit scalaire, soit f une application dérivable de

dans

telle que pour tout
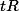
,
\parallel =1)
Montrer que pour tout t dans R, f et f' sont orthogonaux.
J'ai calculé le produit scalaire mais je tombe sur
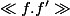
= f.f', ça ne mène à rien.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 21 Jan 2018, 21:08
par pascal16 » 21 Jan 2018, 21:08
en dim 1, comme il faut que la norme de f(t) soit 1, il y pas beaucoup de choix, f parcours une partie du cercle unité, exemple :
f(t) =(cos(t), sin(t))
est bien orthogonale à f'(t).
f(t) =( 1;0) marche aussi
La choix de la fonction est très limitée par le choix de || f(t) ||=1 pour tout t

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Jan 2018, 21:37
par Ben314 » 21 Jan 2018, 21:37
Salut,
Ca donne quoi si on dérive (en t) la relation <f(t),f(t)>=1 valable pour tout t ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
shar
- Membre Naturel
- Messages: 75
- Enregistré le: 28 Aoû 2017, 21:12
-
 par shar » 21 Jan 2018, 23:06
par shar » 21 Jan 2018, 23:06
Ah c'est bon merci ben314
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités