Un =
An =
J'ai dèja démontré que An convergente et posons Lim An = a
Prouvez que :
1) Un - 1/(n+1)² <= An <= Un + 1/(n+1)²
2) a =
et en déduire que a = lim Un .
Et Merci D'avance !
Exo d'analyse et suite Intégral
4 messages
- Page 1 sur 1
Exo d'analyse et suite Intégral
par savan-306D » 14 Jan 2014, 12:57
On a
Un =^{k-1}}{k^2})
An =dx)
J'ai dèja démontré que An convergente et posons Lim An = a
Prouvez que :
1) Un - 1/(n+1)² <= An <= Un + 1/(n+1)²
2) a =dx)
et en déduire que a = lim Un .
Et Merci D'avance !
Un =
An =
J'ai dèja démontré que An convergente et posons Lim An = a
Prouvez que :
1) Un - 1/(n+1)² <= An <= Un + 1/(n+1)²
2) a =
et en déduire que a = lim Un .
Et Merci D'avance !
par Ben314 » 14 Jan 2014, 14:43
Posons =\sum_{k=1}^{n}\frac{t^{k}}{k^2}\)
(polynôme) de façon à avoir )
.
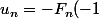On a alors=\sum_{k=1}^{n}\frac{t^{k-1}}{k}\)
et\Big)=\sum_{k=1}^{n}\, t^{k-1}=\frac{1-t^n}{1-t}\)
pour tout 
.
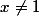
Donc, pour tout
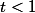
, =\int_0^t\frac{1-u^n}{1-u}\,du+Cst=\int_0^t\frac{1-u^n}{1-u}\,du\)
car , lorsque 
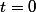
, =0)
.
D'où , pour tout
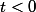
, =-\frac{ln(1-t)}{t}+\varepsilon_n(t)\)
où=\frac{1}{t}\int_t^0\frac{u^n}{1-u}\,du)
On a alors
Donc, pour tout
D'où , pour tout
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par stephaneenligne » 30 Jan 2014, 18:15
j'ai lu en diagonale ton problème : je pense que tu es vraiment proche du but. A partir de l'encadrement présenté en question 1, tu obtiens un encadrement de Un, comme tu sais que An converge, tu peux passer à la limite dans l'inégalité (thm des gendarmes)
par Ben314 » 30 Jan 2014, 21:13
Salut,
Pour tout
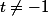
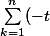on sait que ^{k-1}\ =\ \frac{1-(-t)^n}{1-(-t)}\ =\ \frac{1}{1+t}+\frac{(-t)^n}{1+t})
En intégrant de
à 
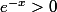
on a ^{k-1}}{k}e^{-kx}\ =\ \ln(1+e^{-x})+(-1)^n\int_0^{e^{-x}} \frac{t^n}{1+t}dt)
Puis, en intégrant de à 
: ^{k}}{k^2}(e^{-kn}-1)\ =\ \int_0^n\ln(1+e^{-x})\,dx+(-1)^n\int_0^n\int_x^{\infty} \frac{e^{-(n+1)u}}{1+e^{-u}}dudx)
C'est à dire^{k}}{k^2}e^{-kn}\ =\ A_n+(-1)^n\int_0^n\int_0^{e^{-x}} \frac{t^n}{1+t}dtdx)
Et... y'a plus qu'à encadrer les deux trucs...
Pour l'intégrale, on peut partir de
pour 
par contre, je vois pas trop quoi faire avec la somme de gauche...
Pour tout
En intégrant de
Puis, en intégrant de
C'est à dire
Et... y'a plus qu'à encadrer les deux trucs...
Pour l'intégrale, on peut partir de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :