[Analyse] Existence d'une primitive

[euler21]

Bonjour
Si on se donne f la fonction caractéristique des rationnels sur le segment [0,1]
est ce qu'il existe une fonction g qui soit la primitive de f sur ce segment ??
Et si oui peut l'exprimer sous forme explicite ??
merci pour vos réponses

[Arkhnor]

Bonjour.

D'après le théorème de Darboux, une fonction dérivée vérifie la propriété des valeurs intermédiaires, ce qui n'est pas le cas de l'indicatrice des rationnels. On en déduit qu'elle n'est la dérivée d'aucune fonction.

[dibeteriou]

Le théorème de Darboux te donne la réponse, après je ne pense pas que ce soit ce que tu attends :we:
Si est dérivable et que est caractéristique des rationnels, que se passe-t-il ?
On a avec entre et (car est dérivable).

Maintenant, fais varier à fixé, et observe ce qu'il se passe.

[euler21]

ok :we:
et si on prend la fonction de l'escalier de diable de Cantor.
je pense que son image est l'intervalle [0,1]
est ce qu'elle admet une primitive ??

[dibeteriou]

Google me dit qu'elle est continue, donc admet des primitives.

[euler21]

j'essaie de penser à une fonction discontinue sur [0,1] en tout point et tque son image soit un intervalle ... :hum:

[dibeteriou]

Par exemple avec l'indicatrice de ? :id:

edit: hum, c'est une grosse bêtise ça :briques:
J'y réfléchis...

[euler21]

si on arrive à diviser [0,1] en deux parties disjointes non dénombrables et denses dont la réunion est [0,1] alors je pense que c'est gagné.
La question c'est comment les expliciter ...

[Arkhnor]

Une telle fonction n'existe pas : l'ensemble des points de continuité d'une fonction dérivée est dense. C'est une conséquence (non triviale) du théorème de Baire.

EDIT : J'ai mal compris la question, je pensais que tu cherchais une fonction discontinue en tout point qui admette une primitive.

[dibeteriou]

Autre idée :
Soit une permutation de , sans point fixe, soit une énumération des rationnels.

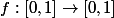
On définit par et si .

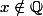
[euler21]

oui je pense que ça marche :id:
la fonction est discontinue partout et son image est l'intervalle [0,1]
maintenant est ce que ta fonction admet une primitive ??

[Arkhnor]

Comme je l'ai dit, une fonction discontinue en tout point n'admet pas de primitives ...

[euler21]

désolé j'avais pas bien vu ton commentaire. Sinon est ce que c'est possible de m'envoyer un lien vers une démonstration de ce résultat ??

[Arkhnor]

Sur Wikipédia, la démonstration est dans la boîte déroulante : http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_la_limite_simple_de_Baire

L'application aux fonctions dérivées est donnée dans la section "Exemple d'utilisation".

Au passage, je ne suis pas certain que la fonction de dibeteriou soit discontinue en tout points, en tout cas, pas pour n'importe quelle permutation sans point fixe.

[dibeteriou]

Au passage, je ne suis pas certain que la fonction de dibeteriou soit discontinue en tout points, en tout cas, pas pour n'importe quelle permutation sans point fixe.

Après réflexion, il y a nettement plus simple en effet :id: