Bonjour,
Je prend P={n ds N| tq Un>0}
Je prend N={n ds N| tq Un<=0}
On montre que P et N forment une partition de N| Et sont infinis.
Ce que je ne comprend pas (ou plutôt je ne sais pas d’où ça sort) c’est que les résultats précédents nous permettent d’affirmer
Qu’il existe alors 2 bijections strictement croissantes f :N| -> P et g :N| -> N,
Pouvez vous me dire cela provient de quel résultat ou théorème ? Merci
Existence bijection strictement croissante
3 messages
- Page 1 sur 1
Re: Existence bijection strictement croissante
Bonjour
Bien sûr ce n'est pas valable pour n'importe quelle suite Un.
Il faut qu'elle prenne une infinté de valeurs positives et une infinité de valeurs négatives comme par exemple
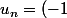^n) ou encore
ou encore 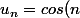) ... etc
... etc
P et N sont deux sous ensembles infinis de l'ensemble
On peut les relier par une bijection à en "numérotant" leurs éléments.
en "numérotant" leurs éléments.
Autre ment dit f(n) est l'indice du (n+1)éme élément de P et g(n) l'indice du (n+1)ème élément de N.
Par ex avec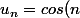)
cos(x)>0
Donc cos(0), cos(1), cos(5) cos(6), cos(7)... sont strictement positifs
Le premiers éléments de P sont 0, 1, 5, 6, 7...
donc si on les "numérote" : f(0)=0, f(1)=1, f(2)=5, f(3)=6, f(4)=7...
même chose pour N et g.
Bien sûr ce n'est pas valable pour n'importe quelle suite Un.
Il faut qu'elle prenne une infinté de valeurs positives et une infinité de valeurs négatives comme par exemple
P et N sont deux sous ensembles infinis de l'ensemble
On peut les relier par une bijection à
Autre ment dit f(n) est l'indice du (n+1)éme élément de P et g(n) l'indice du (n+1)ème élément de N.
Par ex avec
cos(x)>0
Donc cos(0), cos(1), cos(5) cos(6), cos(7)... sont strictement positifs
Le premiers éléments de P sont 0, 1, 5, 6, 7...
donc si on les "numérote" : f(0)=0, f(1)=1, f(2)=5, f(3)=6, f(4)=7...
même chose pour N et g.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
