Exercices polynomes

[jill]

coucou!
dsl ça peut paraitre un peu facil comme exo mais je n'y arrive pas.Voici l'énoncé: montrer que X^3+X+3 est irréductible dans Q.
merci d'avance!

[girdav]

Salut.
je crois qu'il faut raisonner par l'absurde. Tu supposes qu'il existe une racine rationnelle, disons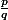 , avec p et q des entiers premiers entre eux.
Ecris le fait que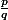 est une racine de .
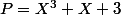Tu devrais obtenir que p divise 3 d'après un théorème sur les divisibilités, et tu montre qu'aucune des diviseurs de 3 n'est racine de P.

[XENSECP]

f(x) = x^3 + x + 3
f ' (x) = 3x^2 + 1 > 0

Donc f a une seule racine

f(x) = (x-a)(x^2+ax+a^2)

Et donc bah

Voilà par exemple... c'est juste analytique mais bon, sinon méthode de Cardan pour retrouver la même chose

[SimonB]

je crois qu'il faut raisonner par l'absurde.

Léon ne sera pas content...

[skilveg]

Pour expliciter la méthode de Girdav: si 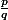est racine de , on obtient 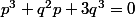donc, si et sont premiers entre eux, ça donne 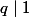et , d'où quatre possibilités (avec ). En testant celles qui sont négatives (-1 et -3), on voit que ce ne sont pas des racines.

Sinon, on peut aussi voir qu'il n'y a pas de racine modulo 2, ce qui est immédiat. (Et un polynôme unitaire irréductible sur l'est sur .)

[Edit: j'ai modifié mon post pendant que ThSQ écrivait le sien...]

[ThSQ]

C'est pas grave il est en vacances là ;) [Edit : je parlais de Léon ! ]


Sinon comme il est de d°3, irréductible <=> pas de racine rationnelle et la soluce de girdav est parfaite.

Encore plus rapide (edit : quoique ...) on peut aussi dire que dans Z/2Z X^3+X+1 est irréductible (pareil, pas de racine) et que donc X^3+X+3 est irréductible dans Z[X] et donc dans Q[X]

(Edit : même soluce que skilveg à la même seconde, les grands esprits ....)

[LeFou.]

Dites; c'est niveau bac + combien sa ? ;D

[ThSQ]

je dirais

[skilveg]

Anecdotiquement, translater la variable pour tenter d'appliquer le critère d'Eisenstein est voué à l'échec (ce qui n'est pas bien grave...). :briques:

[jill]

merci beacoup!!!