Bonsoir à tous,
Je me retrouve avec quelques difficultés face à deux exercices sur les limites.
Voici les énoncés ;
* lim en -infini ((5x² ln(1 - ;)^(1 - x))) / (4x - 7x³)
* lim en 64 ((x^(1/3)-4)/(x^(1/2)-8))^(1/2)
Merci beaucoup
Exercices de limites
8 messages
- Page 1 sur 1
Bonsoir
Tu peux remarquer que) est de la forme
est de la forme )) avec
avec  \to 0) quand
quand  . On peut alors écrire:
. On peut alors écrire:
} {4x - 7x^3}=\dfrac{5x^2} {(- e^{1 - x})(4x - 7x^3)} \times \left[\dfrac{\ln((1 - e^{1 - x})} {- e^{1 - x}}\right])
Quelle est la limite du facteur en crochets? et celle du 1er facteur (faire le changement de variables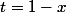 si nécessaire.)
si nécessaire.)
Pour^{1/2}) , poses
, poses 
alimath12 a écrit:Bonsoir à tous,
Je me retrouve avec quelques difficultés face à deux exercices sur les limites.
Voici les énoncés ;
* lim en -infini ((5x² ln(1 -^(1 - x))) / (4x - 7x³)
* lim en 64 ((x^(1/3)-4)/(x^(1/2)-8))^(1/2)
Merci beaucoup
Tu peux remarquer que
Quelle est la limite du facteur en crochets? et celle du 1er facteur (faire le changement de variables
Pour
Bonjour.
Si c'est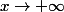 ,OUI.
,OUI.
Il me semble un peu bizarre que vous n'ayez pas vu le changement de variable pour le calcul de limite.
alimath12 a écrit:Il s'agit en effet d'une erreur de ma part, en cherchant à mettre infini, un tiret est venu se glisser.
Puis-je utiliser vos indications malgré cette erreur?
Si c'est
Il me semble un peu bizarre que vous n'ayez pas vu le changement de variable pour le calcul de limite.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
