Exercices compacités d'un ensemble - Topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
haznow
- Messages: 1
- Enregistré le: 17 Jan 2023, 13:21
-
 par haznow » 25 Jan 2023, 07:15
par haznow » 25 Jan 2023, 07:15
Bonjour,
Je bloque sur un exercice en Topologie. Voici la partie de l'énoncé qui nous intéresse :
Pour tous
 \in \mathbb{R}^3~et~m \in \mathbb{R})
, posons
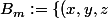 \in \mathbb{R}^3~:~f_m(x,y,z)\leq 1\} = \{(x,y,z) \in \mathbb{R}^3~:~x^2-2xy+2yz+m(2y^2+z^2)\leq 1\})
1. Montrer que
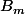
est un compact de

pour tout
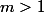
.
Il "suffit" de montrer que
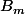
soit un fermé et compact. Le premier point est simple a montrer puisque
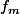
est une application continue.
Mais je n'arrive pas a montrer que ca soit borné...
D'avance merci,
-
mathelot
 par mathelot » 25 Jan 2023, 14:58
par mathelot » 25 Jan 2023, 14:58
Bonjour,
quel est le type de fonction de
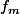
? fonction linéaire,affine, forme quadratique , trinôme ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités