Exercices application linéaires , base , image..

[Raven]

Bonjour , voilà un sujet qui me pose problème


Soit (e1, e2, e3) la base canonique de R3. Soit f : R3 ! R3 lineaire definie par
f(e1) = ;)e1 + e2 + e3, f(e2) = ;)2e1 + 2e3, f(e3) = ;)4e1 + e2 + 4e3.
1)Donner A la matrice de f dans (e1, e2, e3).
2)Donner une base de Imf.
3)Pour quelles valeurs de t appartenant à R, l’application lineaire f ;)tIdR3 est une bijection?
4)Donner un vecteur v1 qui est une base de ker(f ;) 3IdR3) et un vecteur v2 qui
est une base de ker(f). Montrer que (v1, v2, e1) forme une base de R3.
5)Ecrire la matrice de f dans cette base.


1)

A (-1 -2 -4
1 0 1
1 2 4 )

aprés je vous avoue que je comprends pas ..

[gdlrdc]

Je ne sais pas ou tu en es dans tes connaissances sur les espaces vectoriels.
En tout cas `{f(e1),f(e2),f(e3)} est un système générateur de imf, mais est-ce une base?
Regarde si par hasard f(e3) n'est pas combinaison linéaire de f(e1) et f(e2), dans ce cas {f(e1),f(e2)} sera générateur de imf et même une base si tu montres qu'ils sont indépendants, à toi de montrer tout ça

[Raven]

pourquoi combinaison linéaire ? j'ai juste appris que im(u) c'est l'image du vecteur de départ , ou que il existe v tel que f(u)=v ..

[alm]

Salut

pourquoi combinaison linéaire ? j'ai juste appris que im(u) c'est l'image du vecteur de départ , ou que il existe v tel que f(u)=v ..

Oui, tu as appris ça, mais on te demande maintenant; non pas de définir Im(u) mais d'en donner une base.
Si tu suis bien les indications de gdlrdc, tu arriveras peut être à trouver une base de Im(u).

[Raven]

je trouves que f(e1), f(e2) , f(e3) sont liés .. ils ne forment pas une base non?

[alm]

Salut:

je trouves que f(e1), f(e2) , f(e3) sont liés .. ils ne forment pas une base non?

Tout à fait !

Alors : essaye de voir si la famille est libre car si oui alors elle sera la base recheerchée car elle est libre et génératrice pour

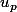Je saisi l'occasion pour rappler que si une famille engendre un sous-espace vectorel d'un espace vectoriel alors si le vecteur est une combinaison linéaire des vecteurs alors la famille est génératrice de .
On se base sur ce principe pour 'enlever' des 'vecteurs' inutils' à une famille génératrice jusqu'à arriver à une famille tel que : lui enlever n'importe quel vecteur fait d'elle une famille non génératrice de l'espace en question. Alors la famille est manifestement une base de .

[Raven]

j'ai fait comme ça : j'ai fait pivôt de gauss avec la matrice en rajoutant à la derniere colonne X , Y , Z . ensuite je trouves X+Z=0 et X=-Z mais la base ensuite je vois pas c'est quoi c'est < ( 1,0,-1) ..