Exercice sur la theorie des corps !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 21 Nov 2009, 14:08
par barbu23 » 21 Nov 2009, 14:08
Bonjour à tous :
Soit

un nombre complexe racine du polynome :
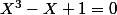
Posons :
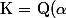 $)
.
Soit :
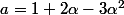
Le corps

est une extension de degré

de

.
 ~~ $)
Determiner les coordonnées de l'inverse de

dans la base
 $)
de
 $)
sur

!
 ~~ $)
Le nombre

est - t - il un carré dans

?
MErci de votre aide ! :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Nov 2009, 14:20
par Ben314 » 21 Nov 2009, 14:20
Méthode bourine (mais pas si longue que ca) :
tu écrit que 1/a=x+y\alpha+z\alpha^2
puis tu dit que 1=a.1/a=... que tu simplifie en tenant compte que
\alpha^3=\alpha-1
il te reste un système de 3 équations à 3 inconues
Méthode plus jolie : tu cherche les polynômes U et V tels que
U(X^3-X+1)+V(-3X^2+2X+1)=1 (bezout... algo d'euclide...)
puis tu réfléchi et tu constate que tu as la solution...
3em méthode (c.f. l'autre discution) :
Tu calcule les coordonnées de a^2 et a^3.
la famille (1,a,a^2,a^3) est forcément liée (car on est en dim 3) tu détermine les coeffs qui lient les 4 vecteur et tu as un polynôme qui annule a (sans doute le polynôme minimal) il ne reste plus qu'a en déduire 1/a (1/2 ligne de calcul)
Je vois pas le rapport entre la question 2) et le reste.
Ce ne serait pas "2 est-il un carré dans Q(\alpha)" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Nov 2009, 16:37
par Doraki » 21 Nov 2009, 16:37
Méthode bourrine-galois :
On utilise la quantitée conjuguée :
Si

,

, et

sont les trois racines de X^3-X+1,
en utilisant les relations coefficients racines,
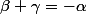
et
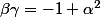
.
On calcule donc la quantitée conjuguée

de a, à savoir
(1+2\gamma-3\gamma^2))
, dans la base
)
Ensuite on calcule

, qui tombe sur un entier, et on a donc calculé
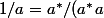)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Nov 2009, 17:00
par barbu23 » 22 Nov 2009, 17:00
Bonjour à tous : :happy3:
J'essaye de suivre les démarches de "Ben312" pour la première question, j'effectue une division Euclidienne suivant les puissances croissantes et voici ce que je trouve, mais je ne suis pas sûr si c'est comme ça qu'on obtient les coefficients

,

et

:

Mais, je ne vois pas comment me debarasser de la partie "Reste" :

Merci de votre aide ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Nov 2009, 17:20
par barbu23 » 22 Nov 2009, 17:20
Ben, tu es là ? je suis complètement perdu ! je sais pas comment me lancer dans ce travail ! :triste: :cry: :doh: :hein: :dodo:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2009, 17:52
par Ben314 » 22 Nov 2009, 17:52
Si tu veux employer la méthode 1 (à mon avis c'est pas la plus jolie...)
tu écrit :
(1+2\alpha-3\alpha^2)=1)
Ensuite tu développe le terme de gauche en utilisant le fait que, par définition,
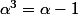
puis, comme
)
est une base tu dit que ce que tu as à gauche doit être

(comme à droite)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
 par mathelot » 22 Nov 2009, 19:05
par mathelot » 22 Nov 2009, 19:05
je me suis demandé:
comme
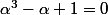
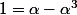
en divisant par

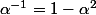
?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Nov 2009, 20:31
par barbu23 » 22 Nov 2009, 20:31
Oui, voilà ! comme je suis très con moi ! Merci de votre secours ! la methode de mathelot est aussi jolie !
Comment faire pour la seconde question ? :happy3:
Merci d'avance ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Nov 2009, 20:35
par barbu23 » 22 Nov 2009, 20:35
LE nombre

n'est pas un carré dans

.
Supposons qu'il existe :

solution de
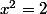
telle que :
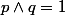
Dans ce cas :
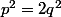
! après que faut-t-il faire pour terminer ? :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Nov 2009, 20:47
par barbu23 » 22 Nov 2009, 20:47

est pair, et donc,

aussi !
Donc

s'écrit :
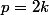
, on remplace dans l'equation de depart , on obtient :
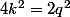
: i.e :
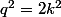
et donc

est pair aussi, donc

et

sont pairs, absurde, car :

et

sont premiers entre eux ! :happy3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 22 Nov 2009, 20:48
par Doraki » 22 Nov 2009, 20:48
Si 2 était un carré dans K, on aurait alors que Q est inclus dans L = Q(sqrt(2)), lui-même inclus dans K.
Je te laisse chercher le degré des extensions [Q:L], [Q:K], et [L:K].

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2009, 21:06
par Ben314 » 22 Nov 2009, 21:06
EUHHH, barbu, la soluce de mathelot est parfaitement juste, mais il me semblait que c'était "a" que tu cherchais à inverser et pas "alpha"....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Nov 2009, 21:40
par barbu23 » 22 Nov 2009, 21:40
Ben314 a écrit:EUHHH, barbu, la soluce de mathelot est parfaitement juste, mais il me semblait que c'était "a" que tu cherchais à inverser et pas "alpha"....
Ah oui, c'est vrai ! :hum: :marteau: :happy2:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 22 Nov 2009, 22:00
par barbu23 » 22 Nov 2009, 22:00
Doraki a écrit:Si 2 était un carré dans K, on aurait alors que Q est inclus dans L = Q(sqrt(2)), lui-même inclus dans K.
Je te laisse chercher le degré des extensions [Q:L], [Q:K], et [L:K].
Oui alors :
] = 2 $)
( le polynome minimal est :

)
] = 3 $)
( le polynome minimal est :

)
Par contre :

combien ? :hum:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Nov 2009, 23:11
par Ben314 » 22 Nov 2009, 23:11
Justement, c'est bien là que le bas blesse.
Si tu ait trois corps : Q contenu dans L lui même contenu dans K et que tu connait [Q:L] et [L:K] , essaye de voir combien vaut [Q:K] (ici le plus simple est de réfléchir en terme de dimensions d'e.v : tout élément de K s'écrit de facon unique comme combinaison linéaire à coeffs dans L d'éléments de la base de K sur L ; tout élément de L ...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 23 Nov 2009, 13:40
par barbu23 » 23 Nov 2009, 13:40
Oui, mais, je ne vois pas comment proceder pour ce type de solution ! :happy3: :hein:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2009, 17:55
par Ben314 » 23 Nov 2009, 17:55
Bon, je "vend la méche" : on a [Q:K]=[Q:L]x[L:K] donc ici, si K était contenu dans L, on aurait : 3=2x[L:K] !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités