bonjour je ne suis pa arriver a faire la question b
http://img15.hostingpics.net/pics/71547420141108205029.png
et voici la correction fait dans un site que je n'ai pas compri merci de me l'explique
http://img15.hostingpics.net/pics/36985420141108211007.png
Exercice sur les suites numeriques
3 messages
- Page 1 sur 1
par Ben314 » 08 Nov 2014, 21:26
Salut,
Arrivé à la question b), normalement, on a déjà fait la a) et on sait que la suite_{n\geq 0})
tend vers 0.
Ensuite,}{x\ln(1+x)}\)
où 
qui tend vers 0.
Or, tu as du voir que, lorsque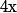
tend vers 0, on a \sim x\)
(équivalent)
Mais aussi que-x\sim -\frac{x^2}{2})
car le D.L. de )
en 0 est =x-\frac{x^2}{2}+\frac{x^3}{3}+...)
Et tu en déduit que}{x\ln(1+x)}\sim \frac{\frac{x^2}{2}}{x\times x}=\frac{1}{2})
lorsque 
(on a le droit de multiplier/diviser des équivalents)
Arrivé à la question b), normalement, on a déjà fait la a) et on sait que la suite
Ensuite,
Or, tu as du voir que, lorsque
Mais aussi que
Et tu en déduit que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :