Exercice sur les carré parfaits. Pouvez vous m'aider

[Allaoui]

Bonjour,

J'ai un exercice sur lequel je suis bloqué,un exercice portant sur le carré parfait. J'ai besoin d'aide.
Voicile sujet :
-----
Soit un nombre x.
Lorsque j'ajoute 22 à x, j'obtiens un carré parfait.
Lorsque je soustraits 67 à x j'obtiens un autre carré parfait.
Que vaut x ?
----
Merci d'avance

[hdci]

Bonjour,

Posez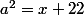 et .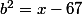

Avec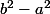 vous faites disparaître x. Il suffit ensuite de factoriser de de voir quels sont les différentes valeurs possibles pour les facteurs. Il n'y a plus qu'à résoudre le système d'équations en a et b.

[Allaoui]

Merci....de mavoir donner cette piste.
Touefois je n'ai toujours pas compris.
Le comblej'y ai refléchi pendant toutes cesvacances de toussaintetlundije dois rendre mon devoir à la maison.
Pouvez vous m'en direun peu pluss'il vous plait ?

[pascal16]

ce qui est proposé est juste l'écriture littérale de ce qu'est un carré parfait, ça ne mange pas de pain d'essayer

que veut a²-b² dans ce qui t'es proposé ?

[Allaoui]

OK.
Que vaut a²-b² ?
a²= x +22
b²= x - 67
a²-b² = x+22 - x +67
a² - b² = 89
(a-b)(a+b) = 89
et c'est là où je bloque, d'autant plus que ce que je cherche à calculer c'est x que j'ai fait disparaitre.

[hdci]

Quels sont les diviseurs de 89 ? (Il n'y en a pas beaucoup !)

Car après, on va avoir a-b = l'un de ces diviseurs et a+b = un autre. Cela fait donc deux équations à deux inconnues, et une fois qu'on a trouvé a et b, on a trouvé x (avec juste un petit calcul à faire).

[Allaoui]

Merci beaucoup à vous deux (Hdci et Pascal16).
J'ai trouvé, x= 2003.

[hdci]

C'est la bonne réponse (facile à vérifier...)

[pascal16]

hdci a fait le boulot, moi j'ai juste servi à motiver

[hdci]

Ne sous-estime pas ton apport pascal16 !

[pascal16]

au passage :
(a-b)(a+b) = 89
vu qu'on cherche a et b positifs et que 89 est un nombre premier, on a une équivalence avec :

a-b = 1
a+b=89

pas de cas négatif qui arrive, ni rien de bizarre