Bonjour je vais essayer d'expliquer ce qui est fait sur ton poly
en fait tu veux étudier la fonction
=100xe^{-0.1x})
pour simplifier un peu on te dit qu'on pose
=e^{-0.1x})
donc
 = 100xu(x))
Tu dérives
; c'est la dérivée d'un produit (
'=u'v+uv')
)donc tu obtiens
=100(u(x)+xu'(x)))
donc en fait on te demande d'abord d'étudier
)
, ce que je refais:
=-0.1e^{-0.1x})
car la dérivée de
})'=g'(x)e^{g(x)})
or
donc
=-0.1u(x))
tu remplaces ensuite dans l'expression de
que tu as trouvé c'est à dire
=
+x(-0.1u(x))))
=
-0.1xu(x)))
ensuite tu mets
en facteurs
=100u(x)(1-0.1x))
mais 100=10*10 donc
=10*10u(x)(1-0.1x))
puis tu "rentres" un de tes 10 dans la dernière parenthèse et tu obtiens
=10u(x)(10-0.1*10x))
d'où
=10u(x)(10-x))
ensuite tu cherches le signe de cette expression ( pour avoir les variations de
)tu as 10>0 , et
>0 car quelque soit x appartenant à R
;
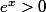
donc le signe de
est le signe de
)
il ne te reste plus qu'à étudier le signe de
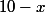
sur [0,36] , qui est donc le signe de
, pour avoir enfin les variations de
voilà j'espère que j'ai pu t'aider sans trop t'embrouiller
