Bonjour à tous, j'ai un souci avec un exercice sur le comptage des dénombrements d'un groupement de

lettres, en particulier la question b)
L'exercice en question :

1
a) La réponse est dans la question, si j'ose dire. Soit la
-e)
lettre apparaît dans un cycle de longueur 2 et alors il y a

choix possibles pour son image, l'image de l'autre lettre du cycle étant forcée, et donc
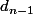
choix possibles pour les

lettres hors du cycle.
Si elle n'apparaît pas dans un tel cycle, alors on a toujours

choix possibles pour son image, et
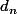
choix possibles pour les

autres lettres.
D'où finalement
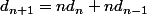
b) C'est là que je bloque un peu
J'ai essayé d'utiliser le critère de D'Alembert pour dire quelque chose sur le rayon de convergence de la série. On a
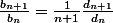
et là j'ai essayé de minorer

puisque
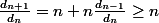
donc

et là on est donc dans le cas où
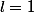
donc on ne peut rien dire ?
Ensuite on pose
 = \sum_{n=0}^{+ \infty} b_n x^n)
et on doit montrer
g'(x) - xg(x) = 0)
là je bloque aussi
On a
 = \sum_{n=1}^{+ \infty} nb_n x^{n-1} = \sum_{n=0}^{+ \infty} (n+1)b_{n+1} x^n)
et
 = \sum_{n=0}^{+ \infty} b_n x^{n+1})
donc on doit finalement montrer :
\sum_{n=0}^{+ \infty} (n+1)b_{n+1} x^n - \sum_{n=0}^{+ \infty} b_n x^{n+1} = 0)
j'avoue que je sèche
Le reste est plus simple
c) D'après l'équa diff on a, lorsque

n'est pas la fonction identiquement nulle, avec

:
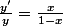
d'où
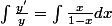
c'est à dire :
| = ln |1-x| - x)
et enfin
 = (1-x)e^{-x})
d'où
 = (1-x)e^{-x})
?
En ce qui concerne la formule :
Pour l'initialisation :
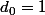
et
^0}{0!} = 1)
--> OK
pour l'hérédité :
soit

un entier, supposons le résultat établi pour tout entier

donc en particulier pour

. Alors on a :
^k}{k!} + n(n-1)! \sum_{k=0}^{n-1} \frac{(-1)^k}{k!} = n n! \left( \sum_{k=0}^{n-1} \frac{(-1)^k}{k!} + n(-1)^n \right) + n! \sum_{k=0}^{n-1} \frac{(-1)^k}{k!}=n!(n+1)\sum_{k=0}^{n-1} \frac{(-1)^k}{k!} + n(-1)^n)
Or
^n = (n+1)(-1)^n - (-1)^n = (n+1)(-1)^n + (-1)^{n+1} = (n+1)! \frac{(-1)^n}{n!} + (n+1)!\frac{(-1)^{n+1}}{(n+1)!})
Soit
^k}{k!} + (n+1)! \frac{(-1)^n}{n!} + (n+1)!\frac{(-1)^{n+1}}{(n+1)!} = (n+1)!\sum_{k=0}^{n+1} \frac{(-1)^k}{k!})
cqfd.
d) On a de façon presque immédiate (en fait c'est une partie du calcul précédent)
^n = n(n-1)!\sum_{k=0}^{n-1} \frac{(-1)^k}{k!} + (-1)^n = n! \sum_{k=0}^{n-1} \frac{(-1)^k}{k!} + (-1)^n + n!\frac{(-1)^n}{n!} = n! \sum_{k=0}^n \frac{(-1)^k}{k!})
Enfin, on reconnaît en
^k}{k!})
le développement en série de la fonction exponentielle en
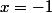
d'où

en

Merci de prendre le temps de lire

