Exercice de suite

[charles xang]

dns de maths aide

[charles xang]

j'ai fait quelques changement de syntaxe pour que ce soit lisible

[charles xang]

pour la 1) faut-il montrer l'injectivité

[Ben314]

Salut,
tu en est où ?

[charles xang]

Salut,
tu en est où ?

je commence et je pense que pour la question il faut utiliser la irationalité de racine de 2, pour montrer déjà que a+b=0 ssi a=0 et b=0 ?

[Ben314]

Oui.
Dans l'équivalence à démontrer, la partie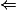 est évidente et, pour la partie , tu essaye d'écrire où les ? sont des entiers et on sait que c'est absurde vu que est irrationnel.

Pour le b) "montrer que la partie... est une parti stable de , il faut que tu montre que le produit de deux éléments de la partie en question donne bien un élément de la partie (simple petit calcul).

Le 2)a) découle immédiatement de la question 1)
Pour le b), tu part de

[charles xang]

Oui.
Dans l'équivalence à démontrer, la partie est évidente et, pour la partie , tu essaye d'écrire où les ? sont des entiers et on sait que c'est absurde vu que est irrationnel.

Pour le b) "montrer que la partie... est une parti stable de , il faut que tu montre que le produit de deux éléments de la partie en question donne bien un élément de la partie (simple petit calcul).

Le 2)a) découle immédiatement de la question 1)
Pour le b), tu part de

JE n'arrive pas le sens indirecte, je suis bloqué à la différence a+B et de a'+b'

[charles xang]

Quelqu'un veut bien m'expliquer commnt faire svp?

[Ben314]

Supposons que sont tels que .
On a donc et, si b-b' était non nul, on en déduirait que ce qui est absurde vu que est irrationnel.
On a donc forcément et on déduit de que

[charles xang]

ah d'accord merci je réfléchis à la question b :)

[charles xang]

donc vu la question A je multiplie a+bracine 2 et a'+b' racine 2 ce qui revient à (a+b racine 2)^2 qui appartient à l'intervalle est ce bon?

[Ben314]

donc vu la question A je multiplie a+bracine 2 et a'+b' racine 2 ce qui revient à (a+b racine 2)^2 qui appartient à l'intervalle est ce bon?

Ben non : y'a rien de correct là dedans.

1) Déjà, je vois pas pourquoi le produit où a,b,a',b' sont des entiers quelconques serait systématiquement égal à

2) Même si c'était le cas, ça ne prouverais rien : les éléments de ton ensemble, c'est tout les réels qui peuvent s'écrire où les deux ? sont des entiers (pas nécessairement égaux) et, à priori, n'est pas de cette forme là.

3) L'ensemble en question, c'est absolument pas du tout un intervalle : il contient clairement tout les entiers (un entier n peut s'écrire : il suffit de prendre a=n et b=0) donc, si c'était un intervalle, ça serait R tout entier (seul intervalle contenant tout les entiers) or, par exemple, il ne contient par (pas trivial à vérifier de façon carré-carré, mais très intuitif il me semble)

[charles xang]

mais comment je fais pour le cas général puisque vous avez pris des valeurs? désolé je ne vois pas je cherche

[Ben314]

où et sont bien des entiers vu que sont des entiers.

[charles xang]

pour la 2)a il faut que je réutilise les réponses d'avant?

[charles xang]

pour la 2)a il faut que je réutilise les réponses d'avant?

on a a, b,b',a' appartenant à Z donc a+b= a'+b' eta+b est une partie stable de Z^2 implique ce qui est demandé à la 2)a)?

[Ben314]

2)a) On as déjà montré que le produit de deux éléments de était lui même dans et donc (mini récurrence évidente) le produit d'un nombre quelconque d'éléments de est lui même dans .

Comme est clairement dans , pour tout entier , est dans ce qui signifie qu'il peut s'écrire sous la forme avec

Enfin on a vu au 1)a) que, lorsqu'un réel peut s'écrire sous cette forme là, l'écriture est unique.

[charles xang]

2)a) On as déjà montré que le produit de deux éléments de était lui même dans et donc (mini récurrence évidente) le produit d'un nombre quelconque d'éléments de est lui même dans .

Comme est clairement dans , pour tout entier , est dans ce qui signifie qu'il peut s'écrire sous la forme avec

Enfin on a vu au 1)a) que, lorsqu'un réel peut s'écrire sous cette forme là, l'écriture est unique.

donc on C^n=an+bn
=an+1 + bn+1
x=an+1 + bn+1
a+b+an+bn=an+1+(bn+1)
an+bn=an+1+(bn+1)-a-b et je trouve les an et bn par identification merci de m'aider :lol3:

[charles xang]

donc on C^n=an+bn
=an+1 + bn+1
x=an+1 + bn+1
a+b+an+bn=an+1+(bn+1)
an+bn=an+1+(bn+1)-a-b et je trouve les an et bn par identification merci de m'aider :lol3:

c'est bien bon?

[Ben314]

Sur le principe, ça a l'air, mais c'est relativement illisible...


Et on en déduit grâce à la question 1)a) que

Profite en pour faire tout de suite le tableau des valeurs de et pour 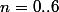(par exemple) qui te permettra de vérifier tes résultats des questions suivantes et de répondre à la dernière question.

je trouve les an et bn par identification merci de m'aider :lol3:

NON : tu ne trouve pas les valeur des trucs "par identification" : ça ne veut rien dire en général et c'est très souvent totalement faux.
Ici, tu en déduit les valeurs des trucs grâce à la question 1)a)