Exercice - suite numérique

[foufa]

slt,
j'ai besoin d'aide voila l'énoncé:
soit f:R-->R une fonction qui admet une limite finie en 0 et qui vérifie f(2x)=f(x) pour tous x de R.
1- montrer que f((2^n)x)=f(x) pur tout x
2-montrer que f constante.

[MathMoiCa]

Salut,

1- montrer que f((2^n)x)=f(x) pur tout x

Par récurrence


M.

[nonam]

Supprimé par la modération - Voir réglement et politique du forum. Premier avertissement

[foufa]

mercie bien

[nonam]

de rien bien !

[foufa]

Merci nonam ,
J’ai trouvé une autre correction mais j’ai pas compris .
L’autre correction :
2^-n (x)--------->0 quand n--->+;)
lim f(2^-n (x))=l
n->+;)
Donc pour tout x de R, f(x)=l
D’où f constante

[nonam]

ah oui, d'ailleurs cette démo est mieux...(le fond reste le même)
grace à la question 1, est une suite constante, et comme sa limite est l, son unique valeur est l, donc f(x)=l.
Est-ce qu'il reste qqch que tu n'as pas compris?

[foufa]

pourquoi n-->f(2^-n(x)) est une suite constante

[Dominique Lefebvre]

ah oui, d'ailleurs cette démo est mieux...(le fond reste le même)
grace à la question 1, est une suite constante, et comme sa limite est l, son unique valeur est l, donc f(x)=l.
Est-ce qu'il reste qqch que tu n'as pas compris?

Voir avertissement ci-dessus.

[nonam]

ben c'est exactement ce que dit la première question :
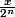
pout tout n, donc f( ) = f() d'où .
Donc

[foufa]

merci je comprend