Exercice sev
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
megurine_luka
- Membre Naturel
- Messages: 45
- Enregistré le: 04 Sep 2010, 11:37
-
par megurine_luka » 16 Sep 2010, 21:48
Bonsoir,
Un petit exercice que je n'arrive pas
[FONT=Arial]E est un espace vectoriel de dimension n sur K et F est un espace vectoriel de dimension p sur K. W est un sous-espace vectoriel de E de dimension q.
A={ u
L(E,F) ; W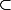
Ker u}.[FONT=Century Gothic]Montre que A est un sous-espace vectoriel de L(E,F) et donner sa dimension[/FONT].[/FONT]
=0_F)
donc l'application nulle appartient à A.
et comment montre-t-on la stabilité?
il faudrait
 \in A^2 \forall \lambda \in K, \lambda u + h \in A)
VOilà je demanderais bien un petit coup de pouce.
Bonne soirée. :++:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 16 Sep 2010, 22:04
L'application nulle est en effet dans A parce que
} = E)
qui contient certainement
.
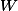
Si tu te donnes une application linéaire de E dans F et un scalaire
, comment comparer le noyau de
et de
?
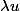
La somme des noyaux et le noyau des sommes?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
