Exercice de proba

[Miko95]

Bonsoir,
J'ai un exercice de probabilité sur lequel je bloque,je cite l'énoncé:

Soit une société qui doit envoyer N lettres à N destinataires.Chaque lettre correspond à un destinataire particulier parmi les N destinataires.
Cette société envoie les N lettres au hasard.
On définit une variable aléatoire X définissant le nombre de destinataires ayant reçu la bonne lettre.Quel est la variance de X?

Je cite ce que j'ai fais:

Je définis une variable aléatoire Xi prenant pour valeur 1 si le destinataire i a reçu sa bonne lettre et 0 sinon.On a donc X=X1+X2+ ... + XN .
Sachant qu'il y a N! façons d'envoyer les N lettres, on a p(Xi =1)= 1/N .
L'espérance E(Xi)= 1/N et on a donc E(X)=N * 1/N = 1 .
Jusque là je m'en sors mais pour calculer la variance je bloque, je voudrais appliquer la formule V(X)=E(X²) - E(X)² mais dans ce cas comment calculer E(X²) ?

Merci d'avance

[fafabzh]

Bonjour,
J'ai l'impression d'après ce que tu as fais que tu es dans le cas d'une distribution, si c'est le cas ta variance doit donc être celle d'une distribution binomiale.

[Miko95]

Merci pour la réponse mais j'ai pas trop compris ce que ça veut dire,à ce que j'ai compris a distribution binomiale c'est lorsque qu'on fait une expérience aléatoire plusieurs fois sachant qu'il y a deux issues possibles, dans ce cas ce serait quoi cette expérience et les deux issues possibles?

[fafabzh]

Merci pour la réponse mais j'ai pas trop compris ce que ça veut dire,à ce que j'ai compris a distribution binomiale c'est lorsque qu'on fait une expérience aléatoire plusieurs fois sachant qu'il y a deux issues possibles, dans ce cas ce serait quoi cette expérience et les deux issues possibles?

L'événement serait : est-ce que le destinataire a reçu sa lettre!
Et la variance se trouve ainsi aisément!!

[nuage]

Salut,
il y a une ambigüité dans l'énoncé. On peut le comprendre de 2 façons :

1. Pour chaque lettre on tire au hasard un destinataire dans l'ensemble {1...N}. Tirage avec remise.
2. On envoie une lettre et une seule à chaque destinataire. Tirage sans remise.

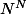Dans le cas 1. il y a possibilités, dans le cas 2. il y en a .

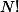Le cas 1. correspond à une loi binomiale de paramètres N et 1/N : on a N envois et pour l'envoi k une proba de choisir le bon destinataire (k) égale à 1/N indépendamment des envois précédents. Dans ce cas le calcul de la variance est facile car les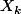 sont des variables aléatoires indépendantes.

Dans le cas 2. les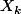 ne sont pas indépendantes et le calcul de la variance est beaucoup plus délicat.

Pour donner un exemple avec N=2
cas 1. on a P(X=0)=1/4 ; P(X=1)=1/2 ; P(X=2)=1/4 et la variance est 1/2
cas 2. on a P(X=0)=1/2 ; P(X=1)=0 ; P(X=2)=1/2 et la variance est 1