Exercice de proba Indépendance
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
slk92
- Messages: 3
- Enregistré le: 03 Déc 2016, 18:57
-
 par slk92 » 03 Déc 2016, 19:09
par slk92 » 03 Déc 2016, 19:09
Bonsoir, je bloque sur cet exo et j'aurai besoin d'aide svp :
Soit (Xn) une suite de variables aléatoires indépendantes et identiquement distribuées telles que :
P(Xn = 1) = P(Xn = -1) = 0.5
Soit N une variable aléatoire suivant une loi de Poisson de paramètre d > 0, indépendante de la suite (Xn).
1) Calculer
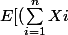^{2}}])
en fonction de n
2) Calculer
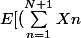^{2}])
en fonction de d
Merci d'avance


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2016, 19:18
par Ben314 » 03 Déc 2016, 19:18
Salut,
Pour le 1), deux méthodes :
- Calculer quelle était la loi de la v.a.r.

et en déduire le truc demandé (un peu long et fastidieux, mais faisable)
- Développer le carré et utiliser les propriétés bien connue de l'espérance (plus joli et plus rapide).
Et j'aurais tendance à t'inciter... à faire les deux...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
slk92
- Messages: 3
- Enregistré le: 03 Déc 2016, 18:57
-
 par slk92 » 03 Déc 2016, 19:27
par slk92 » 03 Déc 2016, 19:27
Merci pour ta réponse,
pour la 1) je trouve n
Mais je bloque plutôt sur la 2...


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2016, 20:08
par Ben314 » 03 Déc 2016, 20:08
Pour la 2), si tu as vu la notion d'espérance conditionnelle et les propriétés associées, ça peut servir.
Sinon, je pense qu'il faut revenir à la définition de l'espérance en terme de probas puis utiliser des proba conditionnelles pour se ramener au cas 1).
Sur le principe, il faut donc écrire (formule des "proba totales") que :
=\sum_{k\geq 0}p(N\!=\!k)\!\times\!p\Big(\sum_{n=1}^{N+1}\!\!X_n\!=\!s\text{ sachant que }N\!=\!k\Big))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
slk92
- Messages: 3
- Enregistré le: 03 Déc 2016, 18:57
-
 par slk92 » 03 Déc 2016, 21:56
par slk92 » 03 Déc 2016, 21:56
Merci pour ta réponse !
Malheureusement je n'ai pas encore vu l'espérance conditionelle
En prépa j'avais vu la formule de Wald pour calcul des espérances de somme dependant de v.a mais ici le carré m'embête...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Déc 2016, 23:15
par Ben314 » 03 Déc 2016, 23:15
Le carré, il pose pas vraiment de problème : ça serait quasiment n'importe quelle fonction, ça ne changerais pas grand chose :
^{2}\Big]=\sum_{s\in{\mathbb Z}}s^2 \times p\Big(\sum_{n=1}^{N+1}{Xn}=s\Big))
puis tu utilise la "formule des proba totale" (c.f. post précédent) pour "casser" la proba ci dessus ce qui te donne une "double somme" et enfin tu re-regroupe les termes différemment pour faire apparaitre les espérances calculées à la question 1.
(en fait, tu démontre sans le savoir un résultat lié aux espérances conditionnelles...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités

