bonsoir
je bloque sur une question de mon devoir :
on suppose A =X^2-2X+1 et D =X(X-1)^2 montrer qu'il existe 3 polynômes R1,R2 et R3 dans R2[X] tels que pour tout polynôme P de R2[X], P= P(0).R1 + P(1).R2 + P'(1).R3
j'ai d'abord pensé à utiliser la formule de Taylor mais je n'aboutissais à rien, est ce que vous pourriez m'éclairer davantage svp ? merci d'avance
(a noter que cette question se situe à la fin d'un exercice traitant de l'application linéaire f où f(P) est le reste de la division euclidienne de AP par D)
Exercice polynômes
9 messages
- Page 1 sur 1
Re: exercice polynômes
Essaye de raisonner par analyse-synthèse, si  et
et 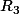 sont tels que
sont tels que 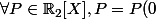R_1+P(1)R_2+P'(1)R_3) , prends pour
, prends pour  un polynôme de degré au plus
un polynôme de degré au plus  tel que successivement :
tel que successivement :
-=1) ,
, =0) ,
, =0)
-=0) ,
, =1) ,
, =0)
-=0) ,
, =0) ,
, =1)
-
-
-
Re: exercice polynômes
je trouve les polynômes (X-1)^2, -X^2+2X et X^2-X
mais je ne vois pas où ça me mène
mais je ne vois pas où ça me mène
Re: exercice polynômes
ah ! comme P(0)=P'(0)= 0, on a P=R1=(X-1)^2 non ? et donc par raisonnement analogue R2=X(2-X) et R3 = X (X-1) ?
Re: exercice polynômes
Exactement, il n'y a qu'une seule possibilité pour les polynômes 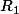 ,
, 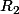 et
et 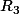 , reste plus qu'à faire la synthèse.
, reste plus qu'à faire la synthèse.
Re: exercice polynômes
(R1 R2 et R3) forme une base de polynômes d'interpolation de Hermite (généralisation de l'interpolation de Lagrange) pour le système d'équations écrit par tuvasbien
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
