Exercice original

par **Imod** » 01 Juil 2007, 18:44

Nuage a pratiquement eu la même idée que moi , j'ai simplement voulu écomiser mes feutres :we:

Imod

par **nuage** » 01 Juil 2007, 18:51

Salut Imod.
C'est bien d'économiser les feutres.
Et je trouve ta solution plus élégante.
Mais pour la réalisation pratique il faut quand même une infinité de feutres (ou un feutre infini). :zen:

par **emdro** » 01 Juil 2007, 19:03

parmi toutes les solutions à ce problème, y en a-t-il une qui minimise la dépense en feutres? :ptdr:

par **Imod** » 01 Juil 2007, 19:20

Il me semble que de toute façon , il va falloir colorier une infinité de points , alors infini contre infini , n'oublions pas qu'il y a un nombre fini d'atomes sur terre ( peut-être même ailleurs ) . On dit aussi que le point n'a pas d'épaisseur :doh:

Imod

par **nuage** » 01 Juil 2007, 19:21

Celle d'Imod colorie un ensemble de mesure nulle et non dense dans R². Je ne crois pas que l'on puisse faire mieux.
En particulier, si on se limite à colorier des courbes, la longueur totales des courbes n'est pas bornée.
Encore que l'on puisse se placer dans le plan projectif, colorier une droite privé d'un point O et une conique de centre O. On peut donc représenter ça sur une sphère et économiser ses feutres. :ptdr:
Du moins il me semble.

par **emdro** » 01 Juil 2007, 19:23

Deux droites sécantes noires avec un point blanc sur chacune et un noir sur la droite définie par les deux points blancs, cela marche aussi, non?

Mais est-ce plus ou moins long que la cible d'Imod? That is the question!

par **Imod** » 01 Juil 2007, 19:30

Il me semble qu'il reste quelques points dont la couleur est à définir ( une parallèle à une droite noire passant par le point noir de la droite blanche ) .

Imod

par **emdro** » 01 Juil 2007, 19:33

Pardon, je n'ai pas précisé que le fond était blanc (toujours une pensée pour mon feutre noir), donc le point noir par lequel j'ai fini mon coloriage est isolé. Toue droite passant par là sera bicolore, non?

par **Imod** » 01 Juil 2007, 19:37

Oui , tu as raison et très économique en plus ( longue vie aux feutres ) !!!

Imod

par **bruce.ml** » 01 Juil 2007, 19:56

J'ai pensé à la même chose que toi Emdro mais il manque une petite chose ! En effet une droite passant par le point blanc d'une de tes deux droites et parallèle à la 2ème serait blanche.
Je propose donc la varieté semi-algébrique définie par :

C'est à dire les deux axes, sans zéro, et le cercle unité

par **emdro** » 01 Juil 2007, 19:59

bruce.ml a écrit:J'ai pensé à la même chose que toi Emdro

Décidément, c'est marrant, j'y avais pensé aussi.

Puis je me suis dit que le cercle était très dispendieux en feutre, et j'ai pensé à cette solution des points blancs... fausse! A vouloir trop faire le malin...

par **bruce.ml** » 01 Juil 2007, 20:12

emdro a écrit:Les deux frérots

:ptdr: :happy2: :ptdr:

par **Imod** » 01 Juil 2007, 20:44

Ces deux là il va falloir les séparer , sinon ça va être le souk !!!

Imod ( prof de collège quasiment en vacances ) .

par **emdro** » 01 Juil 2007, 20:48

on va essayer se se tenir!

Emdro (en vacances s'il n'y avait pas ces satanés jurys de bac demain matin, à perpette, et les joies des oraux du second groupe... :hum: )

par **nuage** » 01 Juil 2007, 20:51

Pour l'économie de feutre et sa mesure :
On définie un homéomorphisme du plan dans le disque ouvert de rayon 1.
Et on calcule la longueur des courbes nécessaires. Dans ce cas elle est clairement bornée. Mais le problème est qu'elle dépend de l'homéomorphisme choisi.
A titre de défi (mais je ne connais pas la réponse) je propose l'homéomorphisme donné au CAPES il y a deux ans (si mes souvenirs sont bons).
On considère le plan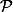

d'équation z=1, la sphère

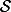d'équation x²+y²+z²=1 et les points O(0,0,0) et S(0,0,-1). L'image d'un point M et le point M" tel que M' est l'intersection de (OM) et

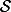et M" l'intersection de (SM') et

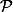. Les images des droites sont des arcs de cercles passant par des points diamétralement opposé dans le disque de rayon 2.
Quelle est alors la borne inf de la longueur des courbes noires telles que toutes droites aient des points noirs et blancs ?
La solution d'Imod n'est pas bornée dans ce cas (elle est donc mauvaise). Celle de Bruce.ml l'est.
Il y a donc de > solutions.
Je vais y réfléchir pendant les vacances.
Et j'espère que le problème vous intéressera. :mur:

A+

par **yos** » 04 Juil 2007, 21:13

Je reviens au problème initiale de Sylar. Il me semble que ça marche si on suppose que les trois angles sont aigus.
J'ai une solution qui me semble intéressante.

par **Sylar** » 04 Juil 2007, 21:28

OUI je veux bien ...

par **Imod** » 04 Juil 2007, 22:19

J'avais renoncé : un problème que l'on annonce difficile , si en plus il faut deviner le problème !!!!

Je regarde quand même avec le triangle acutangle (cela ne semble pas irréaliste , il n'y a que deux couleurs ) ...

Imod

par **Imod** » 05 Juil 2007, 11:28

En attendant une idée pour le problème original :

Imod a écrit:Comment colorier le plan en deux couleurs de façon à ce que toute droite soit bicolore ?

Et si on remplace droite par segment ( non réduit à un point ) ?

Imod

par **Sylar** » 05 Juil 2007, 17:04

Les 3 angles sont forcément aigus non ?

Exercice original

Les deux frérots

Qui est en ligne