Exercice de maths

[claire1999]

Bonjour,

Soit f définie par f(x)= (x^2-x)racine(1-x)

1) déterminer la domaine de définition de Df de f
2) déterminer le domaine sur lequel f est continue
3) La fonction f est-elle dérivable en 1? Justifier
4) Donner l'expression de la fonction dérivée de f
5) Dresser le tableau de variation

Quelqu'un peut-il m'aider ?
Merci beaucoup

[Lostounet]

Bonjour.

Qu'as-tu fait pour commencer?

[claire1999]

J'ai déterminer le domaine de définition qui je crois est R-(1), je ne sais pas comment on fait pour répondre à la question n°2, ensuite la fonction n'est pas dérivable sur 1 car 1 n'est pas compris dans le domaine de définition.
Pour la dérivée, je bloque un peu et donc je ne peux pas faire le tableau de variation

[Lostounet]

Ton domaine ne va pas: f(1) existe ... f(1)=(1^2-1)*racine(1-1)=0*0=0

Ce n'est pas R \ {1} car par exemple f(3) n'existe pas.

c'est quoi la condition pour que racine(1-x) existe?

[claire1999]

c'est si 1-x=0 non ?

[Lostounet]

Non...
Une racine est définie lorsque ce qu'il y a à l'intérieur est positif ou nul.

[claire1999]

ah d'accord ! donc c'est R/(-2) ?

[claire1999]

euh non plutôt R/(2) !

[Lostounet]

Pour quelles valeurs de x est-ce que 1-x est positif ou nul?
C'est à dire 1-x >=0 ?

[claire1999]

pour les valeurs de x >ou=1

[Lostounet]

pour les valeurs de x >ou=1

Tu es sûre?

Il faut résoudre 1-x>=0
Tu peux ajouter x aux deux membres de l'inéquation. Cela donne: 1-x+x >= 0+x
Donc 1>= x

Ce qui signifie que...

[claire1999]

Ce qui signifie que le domaine de définition est sur (-infini;1) ?

[aviateur]

Bonjour C'est pas précis ta réponse.
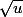est définie ssi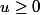

donc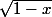 est définie ssi
ssi
Donc le domaine de définition est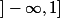 c'est tout de même pas pareil.

[claire1999]

d'accord, merci beaucoup ! et donc que veut dire le domaine de définition sur lequel f est continue ?

[aviateur]

Rebonjour, je ne sais pas en quelle classe tu es, mais ceci :

et donc que veut dire le domaine de définition sur lequel f est continue ?

n'a pas de sens.
Par contre on peut se poser la question de déterminer le domaine de continuité de f.

[Lostounet]

d'accord, merci beaucoup ! et donc que veut dire le domaine de définition sur lequel f est continue ?

S'il y a des mots que tu ne comprends pas dans l'énoncé ou des oublis concernant les domaines de définition (comme tu as oublié pour la racine carrée), pourquoi ne pas avoir près de toi ton manuel scolaire ou sinon un site en ligne avec un vrai cours et des définitions précises?

Personnellement si j'avais devant moi un exercice où je ne comprends pas la question, c'est souvent que je n'ai pas compris une partie du cours...
Quand je comprends la question mais que je ne sais pas faire, c'est là que je demande...

Donc là, à toi de nous dire c'est quoi une fonction "continue" (d'après ton cours). Quel est le domaine sur lequel la fonction racine carrée est continue(cours)?
Quel est le domaine sur lequel la fonction x^2-x est continue? (Cours)

[claire1999]

la fonction x^2-x est continue sur R
la fonction racine carrée est continue sur (0,+infini)

[Lostounet]

la fonction x^2-x est continue sur R
la fonction racine carrée est continue sur (0,+infini)

C'est quoi les parenthèses dans ton intervalle?

En général ( signifie crochet ouvert !
Tu dis donc que racine est continue sur ]0; + infini[ or racine est continue en 0 aussi.

[claire1999]

je n'ai pas les crochets sur mon clavier, mais la parenthèse veut bien dire cochet ouvert

et racine de 1-x est continue sur (-infini;1(crochet fermé) ?

[Pseuda]

Bonsoir,

Oui, la fonction est continue est .