Exercice limites et distributions

[sky]

bonjour,

Je voudrai calculer la limite des fonctions fk(x)=ln(x^2+(1/k^2)) dans D'(R) ( les fk definissent bien des distributions dans R)
On doit donc calculer la limite de l'intégral de la fonction fk mutlipliée par une fonction g appartenant à D(R).
Mon problème est que je n'arrive pas à utiliser le théoreme de convergence dominé pour pouvoir passer la limite à l'intérieur de l'intégral. En fait, je n'arrive pas à majorer ln(x^2+(1/k^2))*g(x) par une fonction ne dépendant pas de k et qui soit convergente.

Merci d'avance pour votre aide.

[tize]

Bonjour,
tu peux décomposer ton intégrale sur par une intégrale sur et une autre intégrale sur 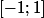pour la première, il n'y a aucun problème puisque les fonction à intégrer sont continues sur l'ensemble d'intégration qui peut être ramené à un compact puisque par définition g est à support compact.
Pour la deuxième il suffit de remarquer que sur [-1;1],

[sky]

je te remercie pour ta réponse mais en fait je ne comprends pas un truc: pour le theoreme de convergence dominé il faut que je majore ln(x^2+(1/k^2))*g(x) par une fonction h ne dependant pas de k et ne dependant pas non plus de l'intégral. Or dans ton explication tu me dis de decouper l'integral en deux... ou alors tu n'es pas en train d'utiliser le theoreme de convergence dominé?? :hein:

merci encore

[tize]

Salut,
oui tu applique le T.C.D. à chacune des intégrales...