Exercice limite 2 (hospital)

[wobot]

Bonjour,
j'ai encore un problème avec ces 2 limites. ^^
Quelqu'un pourrait il m'aider?
Cet fois ci, on peut s'aider de l'hospital SI les méthodes élémentaires ne fonctionnent pas.

Merci d'avance

[zygomatique]

salut

à droite ou à gauche ?

pour la deuxième on prend le logarithme car si x tend vers 0 alors 1 - 2x > 1/2 > 0 pour x suffisamment proche de 0 donc :



l'utilisation d'un dl de ln (1 + h) permet de conclure ...

autre méthode ::

or tend vers ??? quand h tend vers 0

...

[wobot]

Merci pour la réponse mais même avec le ln, ça me fait toujours 1/0 x ln(1-2x) et c'est donc impossible.

[wobot]

Up! please

[zygomatique]

as-tu lu ce que j'ai écrit ?

[aymanemaysae]

Bonsoir,

autre méthode ::

cette assertion m'a désorientée, néanmoins je vous soumets ma démarche qui s'appuie sur la notion des fonctions équivalentes:

Soient les fonctions et ,

comme donc ,

soit aussi la fonction

avec , donc ,

donc ,

donc .

[liryck]

Bonsoir, je me suis penché sur la b :

c'est à dire f(x) = exp()

on cherche à écrire un taux de variation de la forme (f(a+h) - f(a))/h
x-> 0 donc x=h ;




on retrouve donc le taux de variation de ln(-1/2)
or exp(ln'(-2))= exp(-2)
Bon j'avoue il y a un petit soucis de définition avec des ln non définis mais je ne sais pas comment remédier au problème, donc si vous avez une idée je suis preneur.

[Black Jack]

"SI les méthodes élémentaires ne fonctionnent pas."
Reste à voir ce qu'on inclus dans "méthodes élémentaires".

Voila par Lhospital ...
Rien que pour comparer l'efficacité de cette approche par rapport aux "méthodes élémentaires"

*****
lim(x-->1) (x-1-ln(x))/((x-1).ln(x)) forme indéterminée 0/0 --> Lhospital
= lim(x-->1) [(1 - 1/x)/(ln(x) + (x-1)/x)] = lim(x-->1) [(x - 1)/(x.ln(x) + (x-1))] forme indéterminée 0/0 --> Lhospital
= lim(x-->1) [1/(ln(x) + 1 + 1)] = 1/2
*****
f(x) = (1 - 2x)^(1/x)

lim(x--> 0) ln(f(x)) = lim(x--> 0) [ln(1-2x)/x] forme indéterminée 0/0 --> Lhospital
lim(x--> 0) ln(f(x)) = lim(x--> 0) [-2/(1-2x)] = -2

--> lim(x--> 0) f(x) = e^-2
*****

[wobot]

Merci Black Jack!
Est-ce que tu sais comment on fait pour (a)?

[samoufar]

Bonjour,

Je pense qu'on y arrive en utilisant les notions de développement limité et d'équivalents :

Pour la première : On pose et on a en effectuant des DL en 0



Pour la deuxième :

On l'écrit sous la forme , on effectue le DL en 0 de , on en détermine donc la limite en 0, on utilise la continuité de 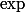en et on conclut que la limite recherchée est .

[zygomatique]

posons f(x) = ln(1 - 2x)

(cours de première)



j'ai été imprécis avec mon "autre méthode"

THE : qui se généralise en bien sur

donc

[Black Jack]

Merci Black Jack!
Est-ce que tu sais comment on fait pour (a)?

Mais je l'ai fait dans le début de ma réponse précédente.

Il fallait quand même remarquer que (1/ln(x) - 1/(x-1)) pouvait s'écrire [(x-1-ln(x))/((x-1).ln(x)) ] ... par une simple mise au même dénominateur.