Exercice équation complexe (examen d'entrée)

[johnnyjohn]

Bonjour tout le monde,
voulant faire des études d'ingénieur civil, je me prépare en répondant au questions des années précédentes. Mais j'ai un léger soucis.
Au départ, je dois résoudre une équation dans C (complexe). On me donne une matrice, je la factorise, etc et j'arrive à :
Après, j'utilise la règle du produit nul. la partie gauche de mon équation (1+i) ne me pose pas de soucis. Donc je m'occuper de la partie de droite, et je pose que z² = t donc j'obtiens une équation du troisième degré. Dès lors, j'utilise Horner et j'obtiens (toujours pour ma partie de droite) (t-1).(-t²-t-2)
Pour mon (t-1) je n'ai pas de soucis. Mais je suis toujours bloqué dans mes résolutions avec (-t²-t-2)
Quelqu'un saurait m'éclairer ?
Merci d'avance

[johnnyjohn]

Enfin, quand je continue. Je calcule le delta de (-t²-t-2)et j'obtiens -7 qui = 7i² donc les racines carrées de mon delta son ainsi pour calculer mes racines. Je fais -> .
Mais après je suis bloqué :/

[fibonacci]

Bonjour;

\\
avec Horner :

[chan79]

Bonjour;

\\
avec Horner :

salut

En poursuivant, les calculs, j'arrive aux 4 solutions:

z =

les réels m et n vérifiant m²=1 et n²=1

[Black Jack]

t²+t+2 = 0 (avec z² = t)

t = [-1 +/- (1-8)^(1/2]/2

t = [-1 +/- (-7)^(1/2)]/2

t = [-1 +/- (7i²)^(1/2)]/2

t = [-1 +/- i.V7]/2

t = -1/2 +/- i.(V7)/2

z² = -1/2 +/- i.(V7)/2

z = a + ib

|z|² = a² + b²

|z²| = V(1/4 + 7/4) = V2

or |z|² = |z²| ---> a² + b² = V2

z² = a² - b² + 2i.ab

a² - b² = -1/2
2ab = +/- (V7)/2

on a donc le système:

a² + b² = V2
a² - b² = -1/2
2ab = +/- (V7)/2

avec a et b des réels

2a² = V2 - 1/2
a² = (2V2 - 1)/4

a = +/- [V(2V2 - 1)]/2

2ab = +/- (V7)/2

+/- V(2V2 - 1) * b = +/- i.(V7)/2

V(2V2 - 1) * b = +/- (V7)/2

b = +/- V7/[2.V(2V2 - 1)]

b = +/- V7.V(2V2 + 1)/[2.V(2V2 - 1).V(2V2 + 1)]

b = +/- V7.V(2V2 + 1)/[2.V(8 - 1)]

b = +/- V(2V2 + 1)/2

z1 = -[V(2V2 - 1)]/2 + i.V(2V2 + 1)/2

z2 = [V(2V2 - 1)]/2 + i.V(2V2 + 1)/2

z3 = [V(2V2 - 1)]/2 - i.V(2V2 + 1)/2

z4 = -[V(2V2 - 1)]/2 - i.V(2V2 + 1)/2

:zen:

[Anonyme]

@Black Jack

écrire (-7)^(1/2) = (7i²)^(1/2) = i.V7 n'est pas "génial" comme explication dite "mathématique"

car d'après "mes connaissances des maths" : la fonction racine carrée est une fonction qui est définie uniquement sur IR+

ps)
à moins que x^(1/2) ne veut pas dire Vx ??

[chan79]

Salut
Black Jack a bien optimisé l'écriture des solutions

z =

avec (m,n) pouvant être (1,1), (1,-1), (-1,1) ou (-1,-1)

[Black Jack]

@Black Jack

écrire (-7)^(1/2) = (7i²)^(1/2) = i.V7 n'est pas "génial" comme explication dite "mathématique"

car d'après "mes connaissances des maths" : la fonction racine carrée est une fonction qui est définie uniquement sur IR+

ps)
à moins que x^(1/2) ne veut pas dire Vx ??

Exactement : x^(1/2) ne veut pas dire Vx

Le signe radical (V) est réservé aux nombres réels positifs.

le x^(1/2) signifie "les racines carrées du nombre x" avec x complexe. (et donc aussi aux réels négatifs)

:zen:

[Anonyme]

@Black Jack

OK no blem....

ps)
Cependant je pense qu'il fallait peut être , quand même , le préciser car en tant que [I]"néophite en maths"

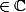
je n'avais pas compris que x quand tu as écris dans ton message : x^(1/2)[/I]