Exercice Dénombrabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
omarel
- Messages: 2
- Enregistré le: 04 Nov 2015, 22:20
-
 par omarel » 04 Nov 2015, 22:26
par omarel » 04 Nov 2015, 22:26
Bonjour
J'ai un DL portant sur la dénombrabilité de R.
pour montrer que R n'est pas dénombrable,on suppose que R l'est, donc on suppose qu'il existe une bijection f de R dans N.
Soit S une partie non vide de R et on pose S'={sigma de 1/2^f(x) x apprtient à A/ tq A partie non vide finie}
Montrez que S' admet une borne supérieur et que 0Merci de répondre je termine l'exercice une fois cette question discutée.
-
Robot
 par Robot » 04 Nov 2015, 22:43
par Robot » 04 Nov 2015, 22:43
Qui est f ?
A partie finie non vide de quoi ?
Quel rôle joue S ?
Ecris un énoncé qui tient debout. Relis-toi avant de poster.
-
omarel
- Messages: 2
- Enregistré le: 04 Nov 2015, 22:20
-
 par omarel » 04 Nov 2015, 22:53
par omarel » 04 Nov 2015, 22:53
Robot a écrit:Qui est f ?
A partie finie non vide de quoi ?
Quel rôle joue S ?
Ecris un énoncé qui tient debout. Relis-toi avant de poster.
La bijection c'est f
A une partie non vide finie de S
S une partie non vide de R
-
Robot
 par Robot » 04 Nov 2015, 22:57
par Robot » 04 Nov 2015, 22:57
Que vaut

?
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 04 Nov 2015, 23:47
par mrif » 04 Nov 2015, 23:47
omarel a écrit:Bonjour
J'ai un DL portant sur la dénombrabilité de R.
pour montrer que R n'est pas dénombrable,on suppose que R l'est, donc on suppose qu'il existe une bijection f de R dans N.
Soit S une partie non vide de R et on pose S'={sigma de 1/2^f(x) x apprtient à A/ tq A partie non vide finie}
Montrez que S' admet une borne supérieur et que 0<sup(S')=<2 .
Merci de répondre je termine l'exercice une fois cette question discutée.
)
est une partie finie et non vide de

, donc elle admet un plus grand élément
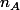
et on a:
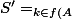} \frac {1}{2^k} \ \leq \ \bigsum_{k =0}^{n_A} \frac {1}{2^k})
Le 2 ème terme de l'inégalité est une somme des
)
premiers termes de la suite géométrique de premier terme 0 et de raison
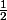
Tu calcules cette somme et tu conclus.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
