Exercice continuité

[Raven]

Bonsoir , voilà un exercice sur la continuité que je n'arrives pas bien à compléter..

Soit f(x) =
cos x/(1 + (x^2) )
Montrer que f est majorée sur R, minorée sur R.
Déterminer Sup f(x) quand x appartient à R

je voulais commencer par dire que cos x est compris entre -1 & 1
mais je sais pas si c'est pareil pour la fonction entiére parce que je divise par 1+x² des deux côtés et ça ne me dit pas les intervalles ..
et le sup je ne comprends pas ..
Merci

[leon1789]

Est-ce qu'il s'agit de ou de ?

[Raven]

la première , pardon je n'ai pas bien écris

[leon1789]

OK.
Comme tu dis, on a .

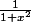
La fraction est-elle bornée ?

[Raven]

comment on sait si elle est bornée ?j'aurai dit par 0&1 mais je sais pas comment le démontrer

[leon1789]

plus grand ou égal à 1 ?

oui


puis sur ?


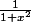
Ensuite, passe à sachant que

[Raven]

1+x²>0 donc 1/1+x² aussi ?

[leon1789]

1+x²>0 donc 1/1+x² aussi ?

c'est vrai mais tu peux faire mieux : ?

[Raven]

plus grand ou égal à 1 ?

[leon1789]

plus grand ou égal à 1 ?

oui


puis sur ?


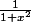
Ensuite, passe à sachant que

[Raven]

inférieur ou égal à 1? donc cosx /1+x² plus petit ou égal à 1
mais pour l'autre borne comment on obtient -1 on a toujours 1/1+x^² plus petit ou égal à 1 non ?

[leon1789]

Soit A un réel coincé entre -1 et 1
tu le multiplies par un réel B positif et plus petit que 1,
alors A.B est plus proche de 0 que A l'est (prends l'exemple B = 1/2),
donc A.B est toujours coincé entre -1 et 1

ici, A = cos(x)
et B = 1/(1+x^2)

[Raven]

donc il faut dire que 0 plus petit égal à -1/1+x²plus petit que cosx/..plus petit égal à 1/1+x² plus petit égal à 1 ?
mais dire que le produit est plus proche de 0 ca revient à dire qu'il est plus grand ou égal à 0?
et sup du coup on fait f(1) vu que c'est un majorant ?

[k000nox]

On sait que : -1 < cos ( x) < 1
et que 0< 1+x^2

On prend sont inverse :

0<1/(1+x^2) <=1
maintenant faut la variation sur R comme ca tu connais le minimun et tu encadre
f(x) = cos(x) /(1 + x^2)

f'(x) = (-sin (x)(x² +1 ) - cos(x) 2 x) / (1+x²)²

[chan79]

donc il faut dire que 0 plus petit égal à -1/1+x²plus petit que cosx/..plus petit égal à 1/1+x² plus petit égal à 1 ?
mais dire que le produit est plus proche de 0 ca revient à dire qu'il est plus grand ou égal à 0?
et sup du coup on fait f(1) vu que c'est un majorant ?

salut
tu peux utiliser les valeurs absolues
|cos x|<=1
1/(1+x²)<=1
donc
|cos x/(1+x²)|<=1
donc -1<=f(x) <=1
et on remarque que f(0)=1
le minimum est atteint pour un x (et son opposé) tel que 2,5437<x<2.5438

[Raven]

d'accord merci beaucoup j'ai compris

[ED102]

Bonjour,

Je dois démontrer en usant de la definition de la continuité que

soit a un réel, pour tout > 0 , trouvez un eta > 0 tel que : |x-a| |sinus(x)-sin(a)| 0
Je commence par |sinus(x)-sin(a)| 0
- Je calcule |f(x)-f(a)|
- Je suppose |x-a|<eta
- Je choisis eta tel que : eta=<;)

Merci de vos conseils.