Exercice complexe - alignement

[Jonny]

Salut, je coince sur un exo que je dois rendre depuis un bon moment.

Déterminer z tel que M(z) , I(i) et M'(iz) soient alignés.

Voilà ce que j'ai fait :

Soit D la droite passant par M et I. Elle a pour vecteur directeur u(z-i).
On a



Après quelques transformations, on obtient :



Jusque là je pense avoir bon.
J'ai essayé d'y voir une équation de droite en écrivant tout ça :



Merci si vous pouvez m'aider

[Luc]

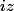
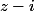
On cherche le lieu des points tels que , et soient alignés. En terme de vecteurs, on peut écrire que le déterminant de et est nul. Que vaut il en fonction des parties réelles et imaginaires de ?
L'ensemble solution est simple. As-tu une idée de ce qu'il peut être (droite, cercle ...). Y a-t-il des points dont tu sais qu'ils appartiennent à cet ensemble?

[Jonny]

Des points qui appartiennent à cet ensemble, rapidement, je vois déja i, 1 et 0. Vu que ces trois points ne sont pas alignées, je verrais plutôt un cercle.

En ce qui concerne le déterminant, si je ne me trompe pas, j'ai

Re(z)*Im(iz-i)-Re(iz-i)*Im(z-i)=0

Donc (Re(z)^2-i*Re(z))+(Im(z)^2-i*Im(z))=0

Merci

EDIT : Suite de mes recherches, j'espère que ce que j'ai marqué plus haut n'est pas faux :hum:

Un complexe z est nul ssi Re(z)=0 et Im(z)=0

J'obtiens donc Re(z)^2-i*Im(z)=0 et Im(z)^2-i*Re(z)=0
Je continue de réfléchir ^^

ReEDIT : Ca marche pas pour 1...

[Luc]

Salut,
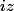
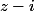
Je ne suis pas d'accord avec l'expression de ton déterminant. Si on note la partie réelle et la partie imaginaire de , que valent celles de ? Les vecteurs et valent donc ...

[Jonny]

Re(iz)=-Im(z) et Im(iz)=Re(z)

z-i=Re(z)+i(Im(z)-1)

iz-i=-Im(z)+i*(Re(z)-1)

J'ai repéré déjà une erreur, je sais pas si c'est la seule. (ou si carrément ma manière d'exprimer mon déterminant est fausse, j'utilise xy'-x'y)

(Re(z)*(Re(z)-1)-(Im(z)-1)*(-Im(z))=0

EDIT : Ca m'a l'air de mieux marcher.

Ca me donne Re(z)^2-Im(z)^2=Re(z)-Im(z)
Donc (Re(z)-Im(z))*(Re(z)+Im(z))=Re(z)-Im(z)

Deux cas : Re(z)=Im(z) : L'équation est vérifiée, donc z est solution.

Re(z)!=Im(z) : je simplifie : Re(z)+Im(z)=1
Solution : Droite d'équation y=-x+1

En tout, deux solutions y=x et y=-x+1

J'ai bon ?

[Luc]

C'est ça!

Maintenant tu peux conclure facilement, non?

EDIT: Si tu n'es pas sur du résultat, pense à vérifier que certains points bien choisis appartiennent bien à l'ensemble trouvé!
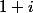
Exemple : Normalement, le point devrait appartenir à l'ensemble trouvé... Pourquoi?

Ou inversement, prend des points particuliers de l'ensemble trouvé, et vérifie qu'ils possèdent bien la propriété d'alignement.

[Jonny]

J'ai conclu en édit sur le post précédent ^^

Je pense que j'ai bon, non ?

Merci beaucoup, ça fait plaisir d'aboutir :)

EDIT : J'ai oublié un moins... J'y retourne... :mur: :mur:

Sauf n-ième erreur d'inattention Ca fait y=-x et y=1-x, non ?

[Luc]

Je ne suis pas d'accord avec ça:

En tout, deux solutions y=x et y=-x+1

Attention aux signes, surtout devant le qui change radicalement la nature de la solution!
Tu as presque la solution, il manque juste une ligne après celle-ci!

[Jonny]

Même après ma rectification tu n'es pas d'accord ?

J'avais zappé le - devant le dernier Im(z).

Mais là je ne crois plus avoir fait d'erreur ^^

Encore une fois, merci !

EDIT : Ma rectification vient après ça,

"J'ai oublié un moins... J'y retourne...

Sauf n-ième erreur d'inattention Ca fait y=-x et y=1-x, non ?"

Comment transformer un forum en chat par edit interposés ^^

[Luc]

Salut,

Reprends tranquillement le calcul où tu l'as laissé:

(Re(z)*(Re(z)-1)-(Im(z)-1)*(-Im(z))=0

.

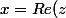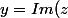Et puis, c'est plus simple à mon goût de noter comme d'habitude et , ce qui fait



Quelle équation obtiens-tu ?

[Jonny]

Ah oui, je suis allé trop vite.. J'ai voulu changer le - direct, sauf que ça marche pas :briques:

Je reprends : J'obtiens

Je transforme en (x-1/2)^2+(y-1/2)^2=1/2

C'est le cercle de centre 1/2 + i/2 et de rayon 1/racine(2)
Ce qui est en adéquation avec ce que j'avais pensé au début : cercle passant par 0, 1 et i.

Ouf, j'espère que c'est bon là(quoique maintenant je ne suis plus sûr de rien). Merci de ta patience, moi qui n'en ai pas et qui veux trop aller vite.

[Ourfalli]

Salut,
Je pense que vous êtes sur la bonne voie, j'ai trouvé une solution similaire.
z, i et iz sont alignées ssi :
et sont alignés, c'est à dire ssi
Ceci mène à :
. (bien sûr : )
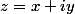
Vu que la partie imaginaire est nulle, on arrive à :
Il faudrait trouver la courbe (plutôt les courbes) correspondant à cette equation, s'agit-t-il d'une conique ?

[Ourfalli]

Un cercle!
Ca m'est passé sous le nez... :doh:
,

[Luc]

C'est le cercle de centre 1/2 + i/2 et de rayon 1/racine(2)
Ce qui est en adéquation avec ce que j'avais pensé au début : cercle passant par 0, 1 et i.

C'est exactement ça!
Ce qu'il faut retenir de cet exo: pour exprimer que trois points sont alignés, tu peux écrire qu'un certain déterminant est nul, ou bien qu'un certain quotient, ici est réel, ce qui revient au même. Exprime que la partie imaginaire du quotient est nulle et tu retrouvera la même équation en fonction de et !