Je ne parviens à résoudre l'exercice suivant :
Soient
a)
Je sais que
Exercice de calcul intégral
5 messages
- Page 1 sur 1
Exercice de calcul intégral
par Jimm15 » 18 Sep 2012, 20:31
Bonjour,
Je ne parviens à résoudre l'exercice suivant :
Soient\in \mathbb{R}^2)
tel que 
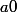
. Montrer :
a)\le \frac{1}{M} \int_{a}^{b} f(x)\text{d}x +m\int_{a}^{b} \frac{1}{f(x)}\text{d}x \le \left(1+\frac{m}{M}\right)(b-a))
Je sais que\le \int_{a}^{b} f(x)\text{d}x \le M(b-a))
.
Je ne parviens à résoudre l'exercice suivant :
Soient
a)
Je sais que
par Luc » 18 Sep 2012, 21:11
Salut,
pour la minoration :
en utilisant l'inégalité bien connue
, on obtient \text{d}x} \sqrt{\int_{a}^{b} \frac{1}{f(x)}\text{d}x} \le \frac{1}{M} \int_{a}^{b} f(x)\text{d}x +m\int_{a}^{b} \frac{1}{f(x)}\text{d}x)
On en déduit la minoration voulue par Cauchy-Scwarz.
pour la majoration, une majoration naïve montre\text{d}x +m\int_{a}^{b} \frac{1}{f(x)}\text{d}x\le 2(b-a))
. Je cherche pour l'affiner.
pour la minoration :
en utilisant l'inégalité bien connue
On en déduit la minoration voulue par Cauchy-Scwarz.
pour la majoration, une majoration naïve montre
par alm » 19 Sep 2012, 23:04
Salut
Une idée pour le faire est de developper)(f(x)- m))
, diviser par )
: il s'agit d'une quantité positive. En integrant de 
à 
on obtient l'inégalité désirée.
Luc a écrit:Salut,
Je cherche pour l'affiner.
Une idée pour le faire est de developper
par Luc » 19 Sep 2012, 23:21
MOHAMED_AIT_LH a écrit:Salut
Une idée pour le faire est de developper
Effectivement, bien vu!
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :