Exercice avec les suites convergentes...j'arrive pas...

[lomdefer]

Bonjour tout le monde, voici l'énnoncé de mon exercice que je n'arrive pas à faire :



Si quelqu'un pouvait m'éclairer sa serait bien cool !!

A+

[tize]

tu n'arrive pas à faire quelle question ?

[lomdefer]

Ben déja j'en suis qu'à la première donc voila...je n'arrive pas à la première.

[lomdefer]

Déja je pense que pour montrer qu'elles convergent il faut montrer que ces deux suites sont des suites de cauchy car tout suites de cauchy est convergente.
Mais je n'arrive pas à montrer qu'elles sont de cauchy(ce qui serait déja une première étapes).

[sandrine_guillerme]

Salut ,

Pour montrer que 2suites adjacentes tendent vers la meme limite revois ton cours ;)

[tize]

essaye plutôt de montrer que est croissante et majorée et décroissante et minorée ...

[lomdefer]

Ben c'est ce que je fait...

[sandrine_guillerme]

Si quelqu'un pouvait m'éclairer sa serait bien cool !!

Pour la question 2/ a , b c revois le principe d'Archimède , le théoréme des petits pas , ou la densité de Q dans R
A+

[lomdefer]

Pour montrer que deux suites adjacentes sont toutes deux convergente de même limite il faut commencer par quoi ?

Déja on sait que : Un+1 >= Un
Vn+1<=Vn et que

lim(Vn-Un)=0
n---->+oo

Voila je connais les ddéfinitions mais j'arrive pas à aller plus loin...

[tize]

Oui c'est très bien, montre maintenant que cela nous oblige à avoir

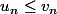
[lomdefer]

aaaaa j'y arrive pas !!!
Déja j'ai compris que si on a Un<=Vn cela veut dire que Un est majoré par le plus petit des Vn.
Mais j'arrivbe pas a prouver que Un<=Vn...

[lomdefer]

Déja si j'ai compris, le but de l'exo c'est de montrer que Un et Vn sont adjacentes.
Donc pour la première question, il faut montrer que Un+1>=Un en faisant la différence entre Un+1 et Un et étudier sont signe.Ensuite il faut montrer que Vn+1<=Vn donc on fait pareil que pour Un et Un+1.