Un exercice d'arithmétique

[yos]

Bonsoir.

Je propose l'exercice suivant :

Soit n un entier naturel tel que soit un nombre premier. Démontrer que n est une puissance de 3.

Bon courage.

[ffpower]

Salut!
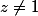
Posons . On constate que P divise ,donc P est produit de polynomes cyclotomiques. Si on suppose que est un nombre premier, alors forcément P est irréductible dans Z : en effet, si ce n était pas le cas l un des polynomes cyclotomiques Q divisant P vérifierait |Q(2)|=1, mais si z est racine de l unité, avec inégalité stricte si , donc le seul polynome cyclotomique vérifiant |Q(2)|=1,c est Q=x-1,mais celui ci ne divise pas P. P est donc irréductible, c est donc le polynome cyclotomique d ordre 3n. En regardant le degré,on doit avoir ,c e qui implique facilement que n est une puissance de 3.

[yos]

Bien joué. On peut aussi rester dans N.

[yos]

P est donc irréductible, c est donc le polynome cyclotomique d ordre 3n.

Tu peux détailler ce point? Pourquoi ne diviserait pas ?

[yos]

C'est bon j'ai compris.

[ffpower]

tant qu on y est,tu peux mettre ta demo?(purement arithmetique si j ai bien compris)

[yos]

, , m non multiple de 3, .
Alors .
Cela entraîne que . Le PGCD de et étant a-1, on a par Gauss , c'est-à-dire , ce qui n'est possible que si , i.e. m=1.

[ffpower]

oki,bien vu aussi,purement arithmetique effectivement :++: