Bonsoir, voilà un petit exo d'arithmétique pas facile je trouve:
"Trouver tous les entiers naturels non nuls tels que n² divise (2^n + 1)"
après quelques essais, il semble que ça marche pour n=1 et n=3. De plus, on doit avoir n impair (bon je sais ça nous avance pas des masses :we: ), voila donc si vous avez quelques idées pour résoudre cet exo ou même pour réduire les conditions que l'on doit avoir, je serais ravi de les lire :happy2:
Bonne soirée
Exercice d'arithmétique
10 messages
- Page 1 sur 1
Bonjour.
J'ai bien l'impression que 1 et 3 sont seuls dans cette catégorie, mais j'arrive juste à prouver ceci :
Le plus petit facteur premier de doit être 3 :
doit être 3 :
En effet, si on appelle ce facteur premier, et si
ce facteur premier, et si 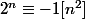 , on a
, on a 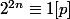 .
.
L'ordre de 2 mod divise donc à la fois
divise donc à la fois  et
et  et il doit donc diviser leur pgcd.
et il doit donc diviser leur pgcd.
 n'est divisible par aucun des nombres premiers qui divisent n. Le pgcd de
n'est divisible par aucun des nombres premiers qui divisent n. Le pgcd de  et
et  est donc 2.
est donc 2.
Pour conclure : le seul nombre premier pour lequel l'ordre de 2 divise 2, c'est 3.
J'ai bien l'impression que 1 et 3 sont seuls dans cette catégorie, mais j'arrive juste à prouver ceci :
Le plus petit facteur premier de
En effet, si on appelle
L'ordre de 2 mod
Pour conclure : le seul nombre premier pour lequel l'ordre de 2 divise 2, c'est 3.
n est (presque) sans facteurs carrés
ReBonjour.
A moins que je ne passe à côté d'une évidence, l'exercice n'est vraiment pas facile.
J'ai montré que était (presque) sans facteur carré :
était (presque) sans facteur carré :
les nombres premiers tels que
tels que 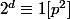 où
où  est l'ordre de 2 modulo
est l'ordre de 2 modulo  , sont extrêmement rares. On n'en connaît que deux : 1093 et 3511 mais personne ne sait démontrer qu'il n'y en a pas d'autre.
, sont extrêmement rares. On n'en connaît que deux : 1093 et 3511 mais personne ne sait démontrer qu'il n'y en a pas d'autre.
(sur ce sujet, voir http://mathworld.wolfram.com/WieferichPrime.html).
En revanche, pour tous les autres, on montre que l'ordre de 2 modulo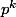 est
est 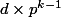 . Je te laisse ceci en exercice.
. Je te laisse ceci en exercice.
A partir de là, si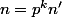 avec
avec =1) ,
, 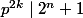 . Donc
. Donc 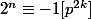 et
et 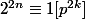 . L'ordre de 2 modulo
. L'ordre de 2 modulo 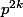 divise donc
divise donc  , c'est-à-dire que
, c'est-à-dire que  divise
divise  . D'où
. D'où 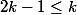 et
et 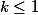 .
.
Un argument similaire à celui de mon précédent message montre que le deuxième plus petit nombre premier qui divise doit être 7 et le suivant est supérieur à 43 (en fait, c'est forcément 43, 127, 337 ou 5419).
doit être 7 et le suivant est supérieur à 43 (en fait, c'est forcément 43, 127, 337 ou 5419).
Voilà... donc pour l'instant, est sans facteur carré (sauf peut-être pour 1093, 3511, et éventuellement quelques autres) et divisible par 21 (si
est sans facteur carré (sauf peut-être pour 1093, 3511, et éventuellement quelques autres) et divisible par 21 (si 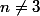 ).
).
A moins que je ne passe à côté d'une évidence, l'exercice n'est vraiment pas facile.
J'ai montré que
les nombres premiers
(sur ce sujet, voir http://mathworld.wolfram.com/WieferichPrime.html).
En revanche, pour tous les autres, on montre que l'ordre de 2 modulo
A partir de là, si
Un argument similaire à celui de mon précédent message montre que le deuxième plus petit nombre premier qui divise
Voilà... donc pour l'instant,
il y a peut-être une autre preuve. mais je suis un peu rouillée, et je ne suis pas certaine de mon raisonnement.
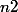 divise
divise 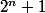
donc il existe un entier k tel que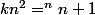
donc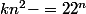
et(\sqrt k n+1)=2^n \qquad (1)$)
on prouve par un raisonnement par l'absurde que est un entier (sinon, il vient de (1) que n n'est pas entier non plus)
est un entier (sinon, il vient de (1) que n n'est pas entier non plus)
donc il existe p et q tels que divise
divise 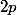
et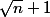 divise
divise 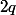
en notant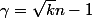
on a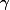 divise
divise 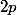 et
et  divise
divise 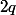
donc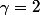 et n est un entier tel qu'il existe k tel que
et n est un entier tel qu'il existe k tel que  donc n=1 ou n=3
donc n=1 ou n=3
donc il existe un entier k tel que
donc
et
on prouve par un raisonnement par l'absurde que
donc il existe p et q tels que
et
en notant
on a
donc
bon, alors, de mémoire, vu que j'ai laissé mes notes sur mon bureau:
supposons que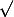 n'est pas entier.
n'est pas entier.
on se souvient de la preuve que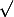 est irrationnel, le résultat est facilement généralisable et connu: si la racine d'un entier n'est pas entiere, elle n'est pas rationnelle non plus.
est irrationnel, le résultat est facilement généralisable et connu: si la racine d'un entier n'est pas entiere, elle n'est pas rationnelle non plus.
donc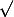 est irrationnel.
est irrationnel.
selon (1), on a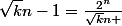
donc$)
et
d'où}{k^2n^2 - k } $)
Or est est un entier, donc n s'écrit sous la forme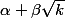 avec
avec 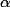 et
et 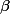 rationnels.
rationnels.
Donc n est irrationnel, ce qui est contradictoire.
supposons que
on se souvient de la preuve que
donc
selon (1), on a
donc
et
d'où
Or est est un entier, donc n s'écrit sous la forme
Donc n est irrationnel, ce qui est contradictoire.
Bonsoir.
Le problème dans la preuve précédente, c'est que le nombre dont le numérateur est égal à -
dont le numérateur est égal à -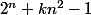 est nul par hypothèse ! Le terme en
est nul par hypothèse ! Le terme en 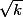 disparait, et on ne peut rien en déduire sur
disparait, et on ne peut rien en déduire sur 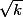 .
.
De toute façons, ce raisonnement n'utilisait pas la forme particulière de l'entier . S'il était valable, on aurait donc démontré :
. S'il était valable, on aurait donc démontré :
Si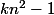 est un entier... alors
est un entier... alors  est un carré ! Ce qui est évidemment faux.
est un carré ! Ce qui est évidemment faux.
Le problème dans la preuve précédente, c'est que le nombre
De toute façons, ce raisonnement n'utilisait pas la forme particulière de l'entier
Si
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
