Exercice td d'analyse intégration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maths62
- Messages: 9
- Enregistré le: 23 Jan 2018, 22:33
-
 par maths62 » 25 Jan 2018, 21:52
par maths62 » 25 Jan 2018, 21:52
Bonjours pouvez vous m'aider à résoudre cette exercice .
f: [a,b]

C une fonction (R)-intégrable
1 On suppose que f est continue et qu'il existe un point t0

[a,b] tel f(t0)

0. Montre qu'il existe un intervalle non trivial [

,

] [a,b] et une constante

>0 tel que |f(t)|


pour tout t

[

,

]
-
Elias
- Habitué(e)
- Messages: 369
- Enregistré le: 07 Fév 2016, 17:20
-
 par Elias » 25 Jan 2018, 22:00
par Elias » 25 Jan 2018, 22:00
Salut,
Par rapport à tous les messages que tu as déjà posté, tu n'as pas avancé avec les indications données ?
f est continue en t0 et f(t0) est différent de 0.
Cela doit te permettre en revenant à la définition de continuité de montrer qu'il existe un voisinage V de t0 (que l'on peut même choisir compact, c'est à dire un intervalle fermé borné) tel que pour tout x dans V, f(x) est différent de 0.
Ce qui doit guider ta preuve " f est continue en t0 donc les f (x) sont proches de f (t0) quand x est proche de t0. Mais à un moment (en prenant x suffisament proche de t0), ils sont tellement proches de f (t0) qu'ils sont forcément eux même différents de 0 (car f (t0) est différent de 0)
Ensuite, que peut-on dire d' une fonction continue sur un compact ?
Pseudo modifié : anciennement Trident2.
-
maths62
- Messages: 9
- Enregistré le: 23 Jan 2018, 22:33
-
 par maths62 » 25 Jan 2018, 22:07
par maths62 » 25 Jan 2018, 22:07
bah le sujet se verrouille donc j'ai pas vue les reponse . Un compact ? c'est la première fois que j'entend se mot moi
-
Elias
- Habitué(e)
- Messages: 369
- Enregistré le: 07 Fév 2016, 17:20
-
 par Elias » 25 Jan 2018, 22:10
par Elias » 25 Jan 2018, 22:10
Un intervalle fermé borné si tu préfères
Pseudo modifié : anciennement Trident2.
-
maths62
- Messages: 9
- Enregistré le: 23 Jan 2018, 22:33
-
 par maths62 » 25 Jan 2018, 22:20
par maths62 » 25 Jan 2018, 22:20
Qu'il existe une subdivision ?
-
Elias
- Habitué(e)
- Messages: 369
- Enregistré le: 07 Fév 2016, 17:20
-
 par Elias » 25 Jan 2018, 22:25
par Elias » 25 Jan 2018, 22:25
Une subdivision de quoi ? Je ne comprends pas...
N'as tu pas vu un théorème qui dit que si f est une fonction continue sur un intervalle [a,b] (fermé borné) à valeurs réelles (ou complexes), alors f est bornée sur [a,b]?
Pseudo modifié : anciennement Trident2.
-
maths62
- Messages: 9
- Enregistré le: 23 Jan 2018, 22:33
-
 par maths62 » 25 Jan 2018, 22:31
par maths62 » 25 Jan 2018, 22:31
Je viens de relire trois fois mon cours la et on l'a pas vue
-
maths62
- Messages: 9
- Enregistré le: 23 Jan 2018, 22:33
-
 par maths62 » 25 Jan 2018, 22:33
par maths62 » 25 Jan 2018, 22:33
On a vue par contre que si une fonction f:[a,b] => est dite bornée s'il existe une constante M tel que quelque soit t appartenant [a,b]: f(t)<=M
-
Elias
- Habitué(e)
- Messages: 369
- Enregistré le: 07 Fév 2016, 17:20
-
 par Elias » 25 Jan 2018, 22:51
par Elias » 25 Jan 2018, 22:51
Ok, bon y'en a pas vraiment besoin...
(tu as oublié une valeur absolue dans ton |f(t)| au passage)
Posons
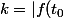| \neq 0.)
f étant continue, la fonction |f| est aussi continue et donc en particulier en t0.
Pour tout
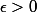
, il existe
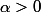
tel que pour tout
| \in [k-\epsilon ; k+\epsilon])
Si tu prends par exemple
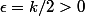
, alors tu as l'existence d'un
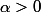
tel que pour tout
| \in [k/2; 3k/2])
En particulier, si tu pose
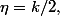
tu as bien pr tout
| \geq \eta)
Pseudo modifié : anciennement Trident2.
-
maths62
- Messages: 9
- Enregistré le: 23 Jan 2018, 22:33
-
 par maths62 » 25 Jan 2018, 23:40
par maths62 » 25 Jan 2018, 23:40
comment on sais que alpha est supérieur à 0 ? et le betta on s'en sert pas ?
-
aviateur
 par aviateur » 25 Jan 2018, 23:46
par aviateur » 25 Jan 2018, 23:46
C'est pas vrai le message n'a pas été verrouillé voir ci-dessous.
https://www.maths-forum.com/superieur/exercice-t191939.htmlC'est la 3ème fois qu'il pose le même exercice sur ce forum. Message qu'il a déjà posé sur un autre forum
et dont certain braves lui ont répondu en partie.
Il ne sait pas du tout mais pas du tout ce qu'est une fonction continue.
Vous pouvez voir que je lui demande d'écrire la définition de la continuité en t_0.
Ce n''est pas la mer à boire. Mais c'est trop fatiguant pour lui.
Alors comment il fait, il repose dans un autre post. Ce qu'il veut c'est une solution toute faite....
-
Elias
- Habitué(e)
- Messages: 369
- Enregistré le: 07 Fév 2016, 17:20
-
 par Elias » 25 Jan 2018, 23:55
par Elias » 25 Jan 2018, 23:55
En effet aviateur...
maths62, c'est pas le même alpha que le tiens que j'ai désigné...
Relis ton cours et travaille les démonstrations pour t'approprier les définitions, je ne peux rien dire de plus.
Bon courage
Pseudo modifié : anciennement Trident2.
-
maths62
- Messages: 9
- Enregistré le: 23 Jan 2018, 22:33
-
 par maths62 » 26 Jan 2018, 09:34
par maths62 » 26 Jan 2018, 09:34
Ah non j'avais pas vue ce message c'est vrai en plus aviateur , je voyais plus mon post la dernière fois
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités