Exercice d'Algèbre

[Maxdu21Eiffel]

Soit E un K-espace vectoriel et f un endomorphisme de E tel que : f^3=f

1) Montrer que : Im(f²) somme direct Ker(f) = E
2) Montrer que : Ker(f) = Ker(fof)
3) Montrer que : Im(f) = Im(fof)
4) Montrer que : Im(f) somme direct Ker(f) = E

Merci de votre aide.

[capitaine nuggets]

Salut !

Soit E un K-espace vectoriel et f un endomorphisme de E tel que : f^3=f

1) Montrer que : Im(f²) somme direct Ker(f) = E
2) Montrer que : Ker(f) = Ker(fof)
3) Montrer que : Im(f) = Im(fof)
4) Montrer que : Im(f) somme direct Ker(f) = E

Merci de votre aide.

1) - Montre pour commencer que l'intersection est triviale (i.e. ).
- Montre que tout élément peut se décomposer sous la forme 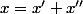où et .

[Maxdu21Eiffel]

Bonjour, pour montrer que Im(f²) inter ker(f) = Oe
J'ai pris un x appartenant à im(f²) inter ker(f)
Donc x appartient a ker f donc f(x)=Oe
ET x appartient à Im(f²) donc il existe un y appartenant a E telle que f²(y)=x

Mais je n'arrive pas a terminer...

[capitaine nuggets]

Bonjour, pour montrer que Im(f²) inter ker(f) = Oe
J'ai pris un x appartenant à im(f²) inter ker(f)
Donc x appartient a ker f donc f(x)=Oe
ET x appartient à Im(f²) donc il existe un y appartenant a E telle que f²(y)=x

Mais je n'arrive pas a terminer...

Oui, je n'ai pas trouver de moyen plus efficace d'y arriver que celui là :
Au lieu de montrer directement que , montre que , puis justifie que .

x appartient à Im(f²) donc il existe un y appartenant a E telle que f²(y)=x

D'ailleurs, tu t'es trompé(e) : :+++:

[chan79]

Bonjour, pour montrer que Im(f²) inter ker(f) = Oe
J'ai pris un x appartenant à im(f²) inter ker(f)
Donc x appartient a ker f donc f(x)=Oe
ET x appartient à Im(f²) donc il existe un y appartenant a E telle que f²(y)=x

Mais je n'arrive pas a terminer...

0=f(x)=f³(y)=f(y)
x=f(f(y))=f(0)=0

sinon tu as
x=f²(x)+(x-f²(x))

f(x-f²(x))=f(x)-f³(x)=f(x)-f(x)=0

[Maxdu21Eiffel]

0=f(x)=f³(y)=f(y)
x=f(f(y))=f(0)=0

Je suis d'accord avec ceci mais la première ligne d'égalité ne donne pas x=OE donc impossible de conclure non?

[capitaine nuggets]

La première ligne sert pour la deuxième à montrer que x=0 :++:

[chan79]

La première ligne sert pour la deuxième à montrer que x=0 :++:

oui
je reprends:
Tu as pris un x appartenant à im(f²) inter ker(f)
donc f(x)=0 et x est l'image d'un y par f² soit f²(y)=x

f(x)=0 peut s'écrire f(f²(y)=0 soit f³(y)=0 soit f(y)=0

ensuite x=f²(y)=f(f(y))=f(0)=0

[Maxdu21Eiffel]

En effet comme ça c'et bien claire merci :)
Maintenant il me reste a montrer que Imf² + Kerf = 0

Faut il faire par double inclusion?

[chan79]

En effet comme ça c'et bien claire merci
Maintenant il me reste a montrer que Imf² + Kerf = E

Faut il faire par double inclusion?

x=f²(x)+(x-f²(x))

f(x-f²(x))=f(x)-f³(x)=f(x)-f(x)=0

[Maxdu21Eiffel]

Je ne comprend pas bien les deux lignes que tu viens d'écrire, peux-tu m'expliquer? Merci beaucoup

[barbu23]

Bonjour, :happy3:
et et , car : ( En utilisant l'hypothèse : )
:happy3:

[Maxdu21Eiffel]

Merci beaucoup de votre ide à chacun. :)

Juste une petite question les égalités de B2 et B3 ne peuvent pas se faire sans hypothèse il me semble? Car il faut le prouver par double inclusion, donc ker(f) incu à ker(f²) pas de soucis et idem pour Im(f²) inclu a Im(f). Par contre les inclusions dan l'autre sens posent soucis si il n'y pas d'hypothèse non?

[chan79]

Merci beaucoup de votre ide à chacun.

Juste une petite question les égalités de B2 et B3 ne peuvent pas se faire sans hypothèse il me semble? Car il faut le prouver par double inclusion, donc ker(f) incu à ker(f²) pas de soucis et idem pour Im(f²) inclu a Im(f). Par contre les inclusions dan l'autre sens posent soucis si il n'y pas d'hypothèse non?

si x appartient à Ker(f²), on a successivement
f²(x)=0
f(f²(x))=0
f³(x)=0
f(x)=0
donc x appartient à Ker f

[Maxdu21Eiffel]

Donc pas besoin d'hypothèse, merci ^^"
Pour Imf inclu à im(fof) c'est la meme chose j'imagine?

[capitaine nuggets]

Donc pas besoin d'hypothèse, merci ^^"
Pour Imf inclu à im(fof) c'est la meme chose j'imagine?

Biensûr que si on a besoin des hypothèses :hum:
- L'inclusion est vraie quel que soit ;
- On a l'inclusion parce que :++:

De manière analogue pour l'image :
- L'inclusion est vraie quel que soit ;
- On a l'inclusion parce que :++:

[Maxdu21Eiffel]

Oui je me suis mal exprimé, je voulais dire pas d'hypothèse autre que celle annoncé dans l'énoncé.
Par contre pour la partie Im(f) inclu dans Im(f²) je n'arrive pas a aller au bout...

[capitaine nuggets]

Oui je me suis mal exprimé, je voulais dire pas d'hypothèse autre que celle annoncé dans l'énoncé.
Par contre pour la partie Im(f) inclu dans Im(f²) je n'arrive pas a aller au bout...

Si alors il existe tel que .
Or vérifie donc en posant , tu as la conclusion voulue :+++: