Bonjour j'aurai besoin de votre aide car je ne vois pas comment répondre à la question 5) de l'exercice d'algèbre ci dessous. J' ai bien entendu déjà répondu au premières questions dont je vous mets les miniatures (cliquer dessus) ou l'abrégé.
On travaille dans
)
, ensemble des matrices carrées d'ordre 3 à coefficients dans C.
I désigne la matrice unité et 0 la matrice nulle.
On pose
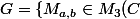 / (a,b) \in C^2\})
où
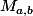
désigne la matrice

1)Montrer que G est un sous espace vectoriel de
)
dont on précisera la dimension et une base; vérifier que G est stable pour le produit matriciel.
(ce que j'ai fait) Page 1 :

Page 2 :

On cherche à résoudre l'équation matricielle (*)
^{2n}-I=0)
, avec M, matrice inconnue, dans G.
On note E le C espace vectoriel

et
)
la base canonique de E.
Soit
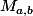
un élément de G tel que
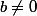
, u l'endomorphisme de E canoniquement associé à M et id l'application identité de E.
2)Déterminer une base de
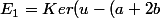.id))
.
Page 3 :

3)Déterminer une base de
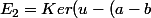.id))
.
Page 4 :

4)Considérons les vecteurs

de coordonnées
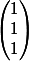
,

de coordonnées
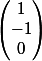
et

de coordonnées

, dans la base B. Montrer que

est une base de E. On la notera B'.
5)Déterminer la matrice D de u dans B'
Je vous remercie.




