évènements corrélés

[beagle]

a la question ce que raconte beagle n'est pas démontrable j'ai répondu si,
par exemple GBZM sait le faire.
c'e'st vraiment sans importance ce passage.

[GaBuZoMeu]

Précisons : je n'ai pas pour le moment de démonstration de P(A_(k+1)|A_k et D) > 1/2.
Beagle a une heuristique, pas encore de démonstration formalisée.
Je ne compte pas formaliser à sa place.

[lyceen95]

Je ne dis pas que Bayes racontait des bétises. Tu as trop fréquenté ton ami Pierre et tu te comportes comme lui.

[beagle]

ce matin en voiture je tombe sur ça:
https://www.francemusique.fr/emissions/ ... 2021-93224

[Vassillia]

Ta présentation me convient donc je la reprends pour essayer de te montrer ce qui peut poser problème. Pour que tous les cas soit faisables à la main, je vais considérer 2n=6 et p=3 (je sais je suis flemmarde) et je note V les bonnes cartes et X les mauvaises cartes.

Les seules distributions acceptables sous la contrainte 4) sont
ou ou ou . Intéressons nous au cas où la plus petite carte 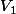est distribuée au premier tour, la plus grande 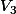au second tour et celle du milieu 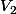au dernier tour, avec ta présentation, cela donne pour les 4 configurations autorisées :
|  | |
  |  |     |

Donc sachant cet ordre ; et ; et
Donc certes la probabilité pour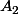 augmente quand on conditionne par et il est facile de demontrer que c'est toujours le cas mais elle reste quand même inférieure à 1/2.

Est-ce grave pour ton heuristique (puisque cela semble convenir à tout le monde) ? Pas forcement, en regardant les 6 ordres possibles et en calculant la probabilité totale, je trouve et et .

Est-ce que c'est grave pour la démonstration ? Un peu quand même car il faut rajouter un conditionnement en fonction de tous les ordres possibles et c'est vite très pénible. En tout cas, je n'ai pas de meilleure idée, on ne peut pas vraiment permuter comme tu le fais puisque des configurations n'existent pas.

Je dis cela dans un but vraiment non polémique, pour tenter d'eclaircir les choses. Le ton nettement plus posé qu'à pris ce fil de discussion est exemplaire et c'est déjà beaucoup je trouve

[beagle]

Vassillia, merci de donner des exemples.
Par contre je ne comprends pas tout.
Déjà du fais du 2n=6 et donc n=3 avec p= 3
donc p=n avec de l'impair mouais j'aurais préféré voir ça en dernier

mais surtout je ne comprends pas de s'interesser à un ordre donné des 3 cartes
couplé à n impair ça fait mal.

tu as fait sur du petit et j'approuve.
Mais monte crescendo dans les particularismes, parce que là je ne reconnais plus le problème.

le plus déstabilisant est un ordre donné des cartes je trouve.

Merci

[Vassillia]

Ça fait mal peut-être mais c'est le jeu ! Un raisonnement doit être valable tout le temps. Je pense qu'il y aura le même probleme dès qu'on fait premiere colonne puis derniere colonne mais c'est plus facile à faire apparaitre sur un cas rapide. Tu peux peut-être déjà essayer de comprendre celui-là quitte à faire toi-même les 5 autres ordres que je n'ai pas détaillé pour mieux visualiser.

Je conditionne sachant l'ordre où sont distribués les plus petits coeurs car cela me donne leur place donc je sais où j'en suis par rapport aux distributions possibles donc je n'ai plus de problème de non équiprobabilité des places restantes. Sans cela, je ne suis pas fichue de calculer les probabilités conditionnelles, il y a peut-être mieux mais j'ai pas. Par contre ce dont je suis sûre, c'est que tu ne peux pas permuter comme tu veux sans respecter certaines contraintes et c'est ce que je voulais te montrer sur des ordres différents qui vont correspondre chez toi aux différentes possibilités de cartes choisies pour Yves au fur et à mesure si j'ai bien compris.

PS : Je te donne le résultat pour un autre cas, si on est sachant ordre (1,2,3) on aura et et

[beagle]

Bonjour Vassillia,
avec 2n=6 et p=3 tout fonctionne correctement.

Par contre utiliser l'ordre c'est soit un autre problème, soit un résultat intermédiaire.
Et tes résultats intermédiaires n'invalident en rien la possibilité de faire sans fixer d'ordre.

Avec tes résultats intermédiaires, calcule proba avoir la premiere, proba avoir la seconde sachant la premiere, proba avoir la troisième sachant les deux premieres.

[Vassillia]

Je ne dis pas le contraire Beagle, évidemment que c'est un résultat intermédiaire qui n'invalide pas l'heuristique, je l'ai même écrit dès mon premier message et je l'ai déjà calculé la proba que tu demandes, relis le, je suis d'accord.

En revanche cela invalide le raisonnement qui dit que quelque soit l'ordre de distribution, la proba sera supérieure à 1/2 et tu t'en sers dans ton raisonnement si je l'ai bien compris. Si tu veux me convaincre qu'en regroupant tous les ordres possibles, on retrouve une probabilité supérieure à 1/2, il faut que tu expliques en quelque sorte que les cas supérieurs à 1/2 compensent les cas inférieurs à 1/2. Oui, je sais, ma phrase n'est pas très mathématiques mais je fais ce que je peux pour faire passer l'idée.

Il est peut-être possible de faire autrement sans tenir compte de l'ordre mais comme je te disais, je ne vois pas et ce que tu proposes ne règle pas le problème comme tu te sers de permutations qui ne sont pas vraiment possibles car elles n'existent pas, elles sont interdites par la contrainte 4).

[beagle]

Tu ne peux pas démolir l'argumentation que je fais avec cette façon de faire.

Je dis lorsque k cœur pour A
cela supprime des cases en B plus nombreuses,
donc j'ai plus de cases pour recevoir la k+1

Alors ensuite vient la non équiprobabilité qui dit que peut-être avec moins de cases candidats en B j'ai plus de combinaisons-permuations-cas.
Et le texte que j'ai mis sur la sixième explique que non,
les contraintes spatiales des candidats k+1 entrainent de nouveau des contraintes spatiales sur la k+2 (et au-delà) qui sont favorables à autant ou plus de combinaisons-permutations-cas pour le joueur A.

Donc pour réfuter ce que je dis, tu dois trouver un cas avec k cœurs placés, et pour la k+1 tu as l'équiprobabilité qui favorise le joueur B.
Si cela existait GBZM l'aurait déjà balancé.

Donc non je ne tombe jamais sous 1/2
en placements déjà pris on est à égalité ou plus de cases interdites en joueur B
en placements à prendre l'équiprobabilité est soit neutre = égalité soit défavorable à B.
Ce sont les contraintes spatiales qui le disent,
pas moi.

[Vassillia]

Je réfute (ou je ne comprends pas peut-être) ta façon de faire. Contrainte spatiale ou pas, il est possible que même s’il y a 2 places de disponibles dans la ligne du haut et 2 places possibles dans la ligne du bas alors le prochain cœur a plus de chances d’arriver dans la ligne du bas. C’est le cas de mon exemple, en imposant le premier cœur dans la première ligne et la première colonne alors le second cœur a plus de chances d’arriver dans la deuxième ligne s'il est à la fin du paquet et je ne vois pas pourquoi il n'y serait pas.
Même si à terme, en regardant tous les cas, il n'y a plus de problème car toujours en imposant le premier cœur dans la première ligne et la première colonne alors le second cœur, s'il est au milieu du paquet, a plus de chances d'arriver dans la ligne du haut. Peut-être que j’ai loupé quelque chose ou peut-être que je m’embrouille avec tous les conditionnements mais il ne me semble pas que GaBuZoMeu ait dit que tu avais raison sur ce point, je te laisse voir avec lui.

[beagle]

Tu peux réfuter ce que je dis,
ou tenter de le faire,
mais là clairement ta réfutation c'est elle qui est fausse par rapport à ce que je dis et fais.

[Vassillia]

Qu'il n'y ait pas de malentendu, je veux bien que la probabilité soit supérieure à 1/2 même si je ne sais pas le démontrer par contre, je ne suis pas d'accord pour dire que ton explication permet de le comprendre. En tout cas moi, je ne vois pas pourquoi cela le justifie car tant que je n'ai pas la proba associée à chaque place disponible, je ne peux rien en déduire du nombre de places disponibles, mais peut-être que d'autres ont compris, je ne me prononce pas à ce sujet.

[lyceen95]

Personnellement, je pense qu'avant de chercher à répondre à une question, il faut s'assurer d'avoir compris la question. Et il faut s'assurer que tout le monde réfléchit sur la même question .
Ici, je ne me hasarderai pas à proposer une réponse, vu que je ne sais pas quelle est la question.

Rassurez-vous, je fais peut-être semblant d'être idiot, mais je ne vous raconte pas le nombre de problèmes professionnels que j'ai pu résoudre, en cherchant à résoudre les quiproquos, en demandant tout simplement aux intervenants de reformuler les questions.

Et pour ça, il faut faire un effort de clarté. Il ne faut pas hésiter à rappeler régulièrement : 'Voici les données du problème, et voici la question'

Un problème bien posé est un problème à moitié résolu.
Henri Poincaré.

[beagle]

Le problème
on distribue à deux joueurs A et B, une par une alternativement les 32 cartes d'un jeu
de 32 cartes dont le random est tel que il n'existe pas deux cartes cœurs consécutives.

On cherchait à connaitre la probabilité qu'un joueur donné mettons A le premier, reçoive les 8 cartes cœur.
La probabilité est connue, a été calculée en combinatoire.

La question qui reste en suspens:
on établit un ordre des cartes cœurs afin de parler de la premiere , de la deuxième, de la kiem carte cœur,

montrez la corrélation positive des évènements :
évènement 1 : la k+1 carte cœur distribuée à joueur A
évènement 2: les 1 à k premiers cœurs distribués à joueur A

comme proba de k+1 est 1/2
il faut montrer que proba( évènement1/ évènement 2) est supérieur à 1/2

en fait plus exactement supérieur ou égal …

PS: pour ceux qui n' y arrive pas il ya un gage
vous tapez Momo Kodama et Debussy ou Chopin et vous devez écouter la vidéo.

[Vassillia]

On est d’accord sur le problème, je me permets juste de généraliser pour que Lyceen95 comprenne mon exemple.
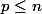On travaille dans D, c’est-à-dire l’ensemble des suites de cartes avec cartes intéressantes disposées de manière à ne pas pouvoir être cote à cote. Sans autre précision, on considère que les suites vérifiant cette condition sont équiprobables donc on peut faire du dénombrement sans se poser de question, jusque là tout va bien.

On dispose les cartes aux emplacements pairs sur la première ligne et les cartes aux emplacements impairs sur la deuxième ligne. Quelle est la probabilité que les p cartes intéressantes soient sur la première ligne ?

On numérote les cartes intéressantes et on note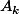 la probabilité d’avoir les premières cartes intéressantes. Beagle pense que et dans ce cas, il peut en déduire que où k+1 indique l'événement avoir la k+1 ème carte intéressante donc les événements seront corrélés positivement.

Beagle veut répondre à la question en disant que lorsqu’on place les cartes intéressantes sur la première ligne alors on bloque des positions de la deuxième ligne de sorte à avoir toujours plus de places libres sur la première ligne que sur la deuxième ligne. Sa remarque est vraie et prouvable sans trop de difficulté, mais ce n’est pas suffisant pour expliquer le problème selon moi. La probabilité d’avoir une carte intéressante n’est pas la même par emplacement (c’est cela le problème de la non équiprobabilité) et donc on ne peut pas conclure directement à partir du nombre d’emplacements libres en haut et en bas. La seule solution que j’ai trouvé, c’est de faire tous les cas possibles pour maitriser cette différence entre les probabilités et bien sur c’est pénible comme tout à généraliser.

PS : bon ben j'espere que c'est de la bonne musique parceque je suis bien parti pour devoir faire le gage

[beagle]

Je ne dis pas seulement ce que tu as écrit.
Il ya plus de cases candidat pour placer des cœurs à joueur A
mais cela n'est pas en équiprobabilité,

je dis depuis plusieurs messages, cette non équiprobabilité , en fait, elle profite à joueur A,
car pour une case donnée en A il y aura autant ou plus de cas

donc on aura à la fois égalité ou plus de cases pour la K+1
ET égalité ou plus de cas-combinaisons-permutations pour ces cases de k+1 en A qu'en B.

Donc meme pas peur de la non équiprobabilité qui est favorable à joueur A.

[lyceen95]

Carte intéressante = Coeurs ... je vais parler des Coeurs, pour rester sur ma terminologie.

L'huissier qui a classé les cartes aléatoirement a vérifié qu'il n'y avait pas 2 coeurs consécutifs.
Il dispose les cartes sur 2 rangées.
Je lui demande de retourner l'as et le 2 de coeur et le 3 de coeur, ils sont tous les 3 sur la première rangée.
Question : Pour chacun des 29 emplacements restants, quelle est la probabilité que le 4 de coeur se trouve sur chacun de ses emplacements.
Il y a quelques emplacements où cette proba vaut 0, parce qu'on sait que 2 coeurs ne peuvent être consécutifs.
Au moins 3 emplacements sont condamnés, entre 3 et 6 emplacements condamnés, selon les cas, et tous sur la 2ème rangée.
Ok clair.
Mais les N emplacements restants ne sont pas équiprobables... là j'ai douté fortement. J'ai douté, puis j'ai été ok avec ça, puis j'ai douté à nouveau.
Je change les données du problème pour essayer de comprendre, et on reviendra au vrai problème ensuite.
On a 10 cartes, et non 32. 4 cartes sont des coeurs et les 6 restantes sont des 'autres'. On a l'assurance que 2 coeurs ne peuvent pas se suivre. Les 3 coeurs qui ont été retournés sont aux positions ???
(1,3,5) (1,3,7) (1,3,9) (1,5,7) (1,5,9) (1,7,9) (3,5,7)(3,5,9)(3,7,9) (5,7,9)
... bon, là, j'ai trop simplifié le problème. Quand j'analyse le dernier coeur, toutes les cases autorisées sont équiprobables.
Je recommence, mais un cran plus tôt :

On a 10 cartes, et non 32. 4 cartes sont des coeurs et les 6 restantes sont des 'autres'. On a l'assurance que 2 coeurs ne peuvent pas se suivre. Les 2 coeurs qui ont été retournés sont aux positions ???
(1,3) (1,5) etc etc
Les emplacements pour le 3 de coeur sont-ils équiprobables, sachant que le 4 de coeur vérifiera encore la contrainte qu'il n'y a pas 2 coeurs consécutifs ...
C'est donc la question en cours... et je comprends mieux ces histoires 'si les premiers coeurs sont sur le début de la rangée ...etc.

[Vassillia]

J’entends ce que tu veux dire Beagle et je pense vraiment que tu as raison, c’est profitable à A mais ce que tu appelles cas-combinaisons-permutations, comme on ne sait pas trop ce qu’on a le droit de permuter ou pas… c’est un peu risqué de bidouiller là-dedans, on pourrait se retrouver à dire des bêtises sans le vouloir même si j’aime ton esprit « même pas peur »

Lyceen95, c’est cela sauf qu’on les présente en 2 lignes donc qu’on on retourne un cœur un haut, en bas, il faut interdire la colonne correspondante et la colonne précédente si tu veux suivre la présentation de Beagle. Malheureusement, il n’y a pas trop de doute, ce ne sera pas équiprobable, regarde mon joli exemple pour t’en convaincre.

[beagle]

Vassillia tu n'es pas perdante a executer le gage:
https://www.youtube.com/watch?v=QIMR4x5nXFM
Debussy lui va super bien aussi mais peu de YouTube, faut aller sur des émissions de France musique pour t'en convaincre.