Etude d'une suite réelle - Maths MPSI

[Inkello]

Bonjour, je suis bloquée moi et ma classe à partir de la question 3, j'espère trouver des pistes de résolution. Merci d'avance.

Voici l'exercice : où u est une suite réelle,
Uo>=0 et quelque soit n € N Un+1 = sqrt(Un)+1/(n+1)

3. On souhaite montrer par l'absurde que la suite u n'est pas croissante.
On suppose pour cela dans cette question que la suite u est croissante.
(a) Démo que Un--> +infini quand n-->+infini
J'ai réalisé une récurrence pour prouver que Un>=n quelque soit n, afin d'encadrer u (minorée par +infini) mais je doute que ce soit une piste fiable..
(b) Etablir une contradiction
La contradiction m'a amenée à avoir Un+1-Un<=0 et non pas >=0 puisqu'elle est supposée croissance, mais encore la je ne suis pas sure.

4.
(a) Justifier qu'il existe p€N tel que Up+1 <Up,
puis prouver que pour tout entier n>=p, Un+1 <Un.
Pour cette question j'aurais aimer trouver le rang p, mais je n'ai aucune piste..
(b) Etudier la convergence de la suite u.
Arrivée ici je suis perdue en vue des questions que je n'ai pas résolues..

Merci de bien vouloir m'aider,

[mathelot]

bonsoir,

c'est


ou

ii) ?

[Inkello]

bonsoir,

c'est


ou

ii)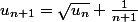

=> C'est : ii)

[lyceen95]

Plutôt que calculer 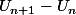, je crois que je calculerais 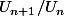et je comparerais ce nombre à 1. Je pense que les calculs sont plus faciles. Mais c'est secondaire.

Recopie l'énoncé clairement.
Que dit la question 3a
Que dit la question 3b.
Recopie mot-à-mot. Si tu changes ne serait-ce qu'un mot, ça devient un autre exercice.

Là, on devine plus ou moins quelles sont les indications de l'énoncé, et quelles sont tes réponses, mais c'est tellement ambigu qu'on ne peut pas t'aider.

Pour la question 4a, je pense que tu ne peux pas trouver le rang p.. Ce rang p dépend probablement de la valeur

Pour la 4b,
Dans les questions précédentes, on t'a demandé de montrer un certain nombre de résultats.
Tu réussis ou pas ces démonstrations, peu importe.
Pour la 4b, tu peux utiliser les résultats des questions précédentes. Tu fais confiance à l'énoncé. En particulier, dans la question 4a, l'énoncé te dit qu'il existe un certain seuil, à partir duquel la suite est décroissante. Tu peux utiliser ce résultat pour la question 4b, même si tu n'as pas réussi à le démontrer.

[Inkello]

J'ai recopié mots pour mots les questions, ce qui est mis en gras, excusez moi si c'est moins lisible, je voulais insérer un fichier mais cela ne fonctionnait pas.

Merci beaucoup en tout cas, je vais voir pour la question 4b.

En tout cas, j'ai indiqué toutes les informations dont je disposais.

[GaBuZoMeu]

Bonsoir,

Je suppose que dans les questions précédentes, on t'a fait montrer que pour tout entier ?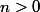

Que peux-tu dire d'une suite monotone, en ce qui concerne sa limite éventuelle ?
Si la suite a une limite finie , peux-tu voir une équation satisfaite par ?

[mathelot]

bonsoir,
si alors pour tout n.

si alors donc L=0 ou L=1

conjecture: si suffisamment grand , alors est décroissante (et minorée par 1 donc convergente vers 1)

[Inkello]

Tout à fait, excusez moi j'ai oublié que oui j'ai prouvé auparavant que Un>=1 et que si Un convergeait vers un réel L, alors L=1

[Inkello]

Le problème c'est que pour prouver que Un tend vers l'infini, on nous propose de raisonner par l'absurde en disant que u est croissante, mais pour prouver qu'elle a une limite non finie, il faudrait que deux suites extraites aient des limites finies ou raisonner par l'absurde mais je ne vois pas comment faire...

[GaBuZoMeu]

Je t'ai posé une question à laquelle tu n'as pas répondu. Je te la repose.

Si j'ai une suite monotone (comme ici la suite dont on suppose qu'elle est croissante), que peut il se passer pour sa limite ? Existe-t-elle ?

(@mathelot : ne te crois pas tenu de répondre à la place de Inkello )

[mathelot]

[Inkello]

Je t'ai posé une question à laquelle tu n'as pas répondu. Je te la repose.

Si j'ai une suite monotone (comme ici la suite dont on suppose qu'elle est croissante), que peut il se passer pour sa limite ? Existe-t-elle ?

(@mathelot : ne te crois pas tenu de répondre à la place de Inkello )

Excusez moi, evidemment que la limite existe, par contre elle peut être finie (si la suite est majorée) ou non finie.

Mais, c'est bien le problème car ici on a une limite non finie, sauf qu'il faut le prouver.

[Inkello]

Puisqu'on a prouvé auparavant que si elle avait une limite finie ce serait L=1..

[GaBuZoMeu]

Bonjour,

Tu as l'air d'avoir trop le nez dans le guidon pour rassembler les morceaux.

On te trace le chemin : montrer par l'absurde que la suite n'est pas croissante.
On suppose donc qu'elle est croissante pour arriver à une contradiction. Puisque'elle est croissante, elle a une limite, finie ou .
Cette limite peut-elle être finie ? Tu as tous les éléments pour répondre avec ce que tu as déjà montré.

[Inkello]

Bonjour,

Tu as l'air d'avoir trop le nez dans le guidon pour rassembler les morceaux.

On te trace le chemin : montrer par l'absurde que la suite n'est pas croissante.
On suppose donc qu'elle est croissante pour arriver à une contradiction. Puisque'elle est croissante, elle a une limite, finie ou .
Cette limite peut-elle être finie ? Tu as tous les éléments pour répondre avec ce que tu as déjà montré.

Oh je vois un peu ! Et bien je dirais que d'après ce que vous me dites cette limite ne peut être finie si la suite est croissante puisqu'on a démontré que si elle était finie L=1 or Un>=1, mais pensez vous que cela suffit comme démonstration afin de démontrer que Un tend vers +infini?

Par ailleurs, la contradiction est simple puisque si j'étudie Un+1-Un ce n'est pas >=0 mais <=0 ?

(Merci beaucoup d'etre patient ^-^)

[GaBuZoMeu]

On a même pour tout .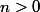
Je pense que tu vois, je te laisse écrire proprement ça pour bien te convaincre.

Par ailleurs, la contradiction est simple puisque si j'étudie Un+1-Un ce n'est pas >=0 mais <=0 ?

Là, ça ne va pas.
Tu peux montrer qu'il y a contradiction avec le fait que la suite est croissante, mais pour cela il est utile de se servir du fait que si la suite est croissante, alors elle tend vers .

[Inkello]

Ok je vois maintenant, par contre, je n'arrive pas à voir où vous voulez en venir au niveau de la contradiction.

En quoi je peux dire que si elle est croissante et tend vers +infini, il y a un problème.. faut-il justifier par le fait que :

- premièrement : si elle converge, c'est vers 1
- deuxièmement : si elle est croissante, elle tend vers +infini

Sachant que Un>=1, c'est impossible qu'elle soit croissante en tendant vers +infini, alors que si elle convergerait, ce serait vers 1 ?

est la bonne piste ?

[GaBuZoMeu]

Je ne vois pas le sens de ce que tu écris.

Je suppose que tu es d'accord qu'on a démontré :
Si alors elle tendrait vers 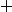(Question 3a)

Pour la question 3b, on doit trouver une contradiction.
Indication : si tend vers l'infini, il est impossible qu'elle soit croissante. Utiliser pour cela la relation de récurrence, et le fait que est plus grand que n'importe quel réel fixé à l'avance, pour suffisamment grand (choisir astucieusement le ).

[Inkello]

Hum ok, grâce à la relation de récurrence, on voit bien que Un+1<=Un, mais je ne vois pas du tout quel M je pourrais choisir.

[GaBuZoMeu]

Hum ok, grâce à la relation de récurrence, on voit bien que Un+1<=Un,

Pourquoi ? Comment le vois-tu ?