Etude d'une intégrale

[Ezra]

Bonjour,

j'ai eu à résoudre :

où

que feriez-vous ?

[Sourire_banane]

Salut,

Bonjour,

j'ai eu à résoudre :

où

que feriez-vous ?

...
Je demande à ma calculatrice ?

Et je ne vois rien à résoudre, sinon une intégrale à calculer.

[Ezra]

Salut,

...
Je demande à ma calculatrice ?

Et je ne vois rien à résoudre, sinon une intégrale à calculer.

quelle est votre démarche sans aide ?

[Sourire_banane]

quelle est votre démarche sans aide ?

Déjà je vois de l'intégrale de Bertrand (si tu n'as pas écrit ln(t^a) ce qui n'a pas d'intérêt car alors on pourrait écrire ça sous la forme a*lnt), par contre pour ce qui est de l'arctan... A première vue comme ça, pas d'idée particulière. Une IPP ce serait fou, un changement de variable, je vois pas.

[Ezra]

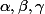
Est-ce que je n'ai pas plusieurs cas à vérifier selon ? Cela me simplifie peut-être la forme...

[Mathusalem]

Bonjour,

j'ai eu à résoudre :

où

que feriez-vous ?

Ils vivent dans quoi tes paramètres ? A priori pour alpha supérieur à 0, ton intégrale diverge toujours (en t = 1 tu divises par 0).

EDIT:

En fait je vois très difficilement moyen que ceci converge. Déjà, tu dois envoyer le ln au numérateur pour virer la singularité en t=1. L'arctangente c'est gentil borné, vaut 0 en t=0. Il faut une puissance résultante inférieure à -1 sur t (gamma/2-beta) pour que ca s'intègre à l'infini, puisque ln est croissante et arctan est bornée. Sauf qu'alors, je pense pas que t'arrives à virer la singularité en t=0 dû au log qui est au numérateur maintenant.

A prendre avec des pincettes... là c'est au feeling.

[Sourire_banane]

Ah oui ton com, Mathusalem, me rappelle que j'ai complètement occulté les critères d'intégrabilité de f sur l'intervalle choisi... :hum:

PS : Et du coup on aimerait bien que ça diverge question de ne pas avoir à primitiver ce machin... :zen:

[deltab]

Bonsoir

Ah oui ton com, Mathusalem, me rappelle que j'ai complètement occulté les critères d'intégrabilité de f sur l'intervalle choisi... :hum:

PS : Et du coup on aimerait bien que ça diverge question de ne pas avoir à primitiver ce machin... :zen:

L'étude de la nature de cette intégrale revient à étudier la nature des intégrales suivantes:
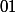
et avec . Si l'une des 4 intégrales diverge, l'intégrale diverge aussi.

[deltab]

Bonsoir

Ah oui ton com, Mathusalem, me rappelle que j'ai complètement occulté les critères d'intégrabilité de f sur l'intervalle choisi... :hum:

PS : Et du coup on aimerait bien que ça diverge question de ne pas avoir à primitiver ce machin... :zen:

L'étude de la nature de cette intégrale revient à étudier la nature des intégrales suivantes:
et

[DamX]

Ils vivent dans quoi tes paramètres ? A priori pour alpha supérieur à 0, ton intégrale diverge toujours (en t = 1 tu divises par 0).

EDIT:

En fait je vois très difficilement moyen que ceci converge. Déjà, tu dois envoyer le ln au numérateur pour virer la singularité en t=1. L'arctangente c'est gentil borné, vaut 0 en t=0. Il faut une puissance résultante inférieure à -1 sur t (gamma/2-beta) pour que ca s'intègre à l'infini, puisque ln est croissante et arctan est bornée. Sauf qu'alors, je pense pas que t'arrives à virer la singularité en t=0 dû au log qui est au numérateur maintenant.

A prendre avec des pincettes... là c'est au feeling.

Bonjour,

En 0 c'est l'arctan qui vient sauver du Log vu qu'il est équivalent à -4t^3.

Si on réécrit f(t)=t^a (ln t)^b Arctan(3t-4t^3),

Comme déjà dit si b>0 (pour éviter la singularité en 1), on est continu sur l'intervalle puis on prend a0 pour tuer le Log avec l'apport d'arctan dans la puissance de t.

Bref avec b>0 et -3<a<1, cette chose est intégrable ... mais ça ne fait pas avancer pour sa valeur

Damien

[Mathusalem]

En reprenant ta notation :



L'équivalent d'arctan en 0 c'est t, pas t^3 (qui est dominé par t)

b>0 forcément pour pas avoir de singularité en 1.

Pour t tend vers 0,
Ça implique a>-1 strictement.
Pour t tend vers , on a
Ça implique a 0, -1<a<0, et une partie cachée de l'énoncé qui dit que les paramètres vivent dans R+

[DamX]

Ouh la oui au temps pour moi ! Il faut a>-1 en 0

Pour t en l'infini, ça implique même a<-1, pour que l'intégrale converge. Et du coup pas de domaine d'existence non ?

[Mathusalem]

Ouh la oui au temps pour moi ! Il faut a>-1 en 0

Pour t en l'infini, ça implique même a<-1, pour que l'intégrale converge. Et du coup pas de domaine d'existence non ?

Effectivement, j'ai eu un léger bug cérébral. Du coup c'est impeccable, ça converge jamais !

[Ezra]

Remplacer par : avec sur : et est en paramètre...