étude de Suites

[Vlad-Drac]

Coucou j'etude la suite defini par
U0=1
Un+1= racine ( 2Un +3)
j'ai commencé par montrer qu'elle etait décroissante. je cherche a savoir si elle est majoré. Quelqun pourrait il m'indiquer une methode ?


merci

[ffpower]

Croissante tu veux dire?
Pour montrer qu'elle est majorée, tu résous et tu montres que ce l est un majorant

[gdlrdc]

Alors déja tu peux dire que Un est définie car positive.
Tu as du te trompé en disant Un décroissante car elle est croissante.
Tu peux montrer par récurrence qu'elle est majorée, en choisissant comme majorant sa limite... a toi de jouer

[Vlad-Drac]

ha oui pardont je me lance pour la suite merci pour le départ

[Vlad-Drac]

bon alors j'ai cherché mais je vois pas trop.
je sais qu'elle est croissante et minorée par 1.
pour montrer qu'elle est majoré je vois pas. on me dit de passer par la limite mais ai je le droit de suposé qu'elle en admet une ? parceque l'idée pour moi aurait été de montré qu'elle est croissante + majoré donc qu'elle converge et ensuite trouver sa limite...

et d'autre part j'ai l'impression que la limite de Un c'est + infini :// :briques:

[Sa Majesté]

Comme l'a dit ffpower, tu résous 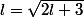et tu montres que ce l (qui est égal à 3) est un majorant
Bien sûr c'est la limite mais tu n'as pas le droit de le dire
Donc tu montres par récurrence que pour tout n, u_n est inférieur à 3 (sorti du chapeau j'en conviens)
Du coup (u_n) est majorée
Comme elle est croissante, elle converge etc etc

[Vlad-Drac]

ha je vois c'est pas mal, merci beaucoup.
Et petite qestion est ce que c'est une bonne idée, si je par en étudiant la fonction racine(2x+3) ?
(je dérive etc etc )

[Ben314]

Pour en "rajouter une couche" sur le fait que tu ne sait pas au départ s'il y a une limite ou pas mais qu'il faut quand même résoudre l'équation, tu peut écrire :
"J'ai montré que la suite est croissante donc, si elle admet une limite l cette limite sera un majorant de la suite.
De plus, comme avec f continue, si la suite admet une limite l alors l vérifie l=f(l).
Tout m'ammène donc à commencer par résoudre l'équation l=f(l) puis à regarder si la (ou une des) solution(s) est bien un majorant de la suite..."

P.S. pour ce genre de suite , on a bien sûr intérêt à étudier f (c'est ce que tu propose) et il peut aussi arriver que l'étude de soit utile en particulier car 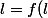équivaut à et que 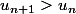équivaut à ...