L1 étude suite récurrente

[Seth]

Bonsoir, comme dit dans le titre mon exercice porte sur l'étude d'une suite récurrente et j'aimerais savoir si une partie de mon raisonnement est juste. En voici l'énoncé :

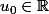
Etudier la suite définie par et .


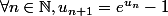
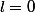
J'ai donc commencé à dire que la fonction récurrente associée à la suite était strictement croissante sur . Elle a pour unique point fixe (qui vérifie l'équation ).
Pour connaître la limite j'ai fait par disjonction de cas sur :

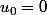
Si alors et ainsi de suite... La suite converge donc vers 0.

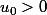
Si , f est croissante sur et non majorée donc la suite diverge vers .

(et c'est là où je ne suis pas sûr pour la démonstration)
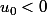
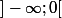
Si , on a f croissante sur et , montrons par récurrence que est majorée par 0 :
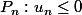
Soit la propriété pour cette démonstration :

Initialisation : 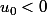(cas étudié) donc propriété P vraie au rang 0.

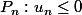
Hérédité : On suppose vraie au rang n, la propriété est-elle vraie au rang n+1 ?
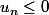
Par hypothèse de récurrence on a alors ,
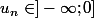
or alors .
Propriété vérifiée donc .

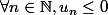
La suite récurrente est croissante et majorée par 0, alors elle tend vers son unique point fixe .

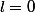
Merci d'avance pour ceux qui m'apporteront leur aide, je vous souhaite une bonne soirée.

[lyceen95]

Tu dis que : la fonction récurrente associée à la suite est strictement croissante.
Je ne connais pas trop cette notion. J'imagine que tu parles de la fonction f : f(x)=exp(x)-1
Ok, elle est strictement croissante.

A la fin de ton raisonnement, tu dis : la suite () étant croissante ...

Ah ? Peut-être que cette suite est croissante. Mais tu ne l'as pas démontré.

[Seth]

La fonction associée à la suite est croissante sur donc la suite est croissante elle aussi non ?

[Seth]

Oui je viens de regarder la suite est croissante. Pour une suite récurrente on m'a dit qu'on pouvait regarder les variations de sa fonction associée, ou regarder le signe de f(u0)-u0.

Si tu as un contre-exemple de suite récurrente croissante qui a sa fonction associée décroissante (resp. décroissante,croissante) je veux bien voir.

[Sa Majesté]

Si tu as un contre-exemple de suite récurrente croissante qui a sa fonction associée décroissante (resp. décroissante,croissante) je veux bien voir.

avec

[Seth]

Merci, est-ce que du coup tu peux me dire ce qui ne va pas avec mon raisonnement ?

[Sa Majesté]

Avec , il n'y a en général aucun lien entre la monotonie de la fonction et celle de la suite.
Avec la fonction racine carrée, croissante, tu as une suite décroissante si , croissante si , et constante si ou .

[Sa Majesté]

Déjà il faut étudier f (variations, limites).
Tu as remarqué un point fixe qui est x=0.
Du coup que peux-tu dire si , si , si ?
Et comment le démontrer ?

[Seth]

Alors il faut re-prouver par récurrence la monotonie de la suite à chaque fois qu'on change de cas (pour ) ?

[Seth]

Déjà il faut étudier f (variations, limites).
Tu as remarqué un point fixe qui est x=0.
Du coup que peux-tu dire si , si , si ?
Et comment le démontrer ?

C'est ce que j'ai fait, j'ai montré vers quoi la suite tendait en fonction de , mais j'imagine que c'est faux ?

[Seth]

Déjà il faut étudier f (variations, limites).
Tu as remarqué un point fixe qui est x=0.
Du coup que peux-tu dire si , si , si ?
Et comment le démontrer ?

Donc pour elle est croissante, pour elle est constante et enfin pour elle est croissante aussi.

[Sa Majesté]

Si alors et ainsi de suite... La suite converge donc vers 0.

OK

Si , on a f croissante sur et , montrons par récurrence que est majorée par 0 :
Soit la propriété pour cette démonstration :

Initialisation : (cas étudié) donc propriété P vraie au rang 0.

Hérédité : On suppose vraie au rang n, la propriété est-elle vraie au rang n+1 ?
Par hypothèse de récurrence on a alors ,
or alors .
Propriété vérifiée donc .

OK

La suite récurrente est croissante et majorée par 0, alors elle tend vers son unique point fixe .

Pas OK car tu n'as pas montré que la suite est croissante (voir mon exemple de la fonction racine carrée).
Il faut étudier le signe de .

[Seth]

La suite récurrente est croissante et majorée par 0, alors elle tend vers son unique point fixe .

Pas OK car tu n'as pas montré que la suite est croissante (voir mon exemple de la fonction racine carrée).
Il faut étudier le signe de .

Du coup ça revient à étudier les variations de et on obtient qu'elle est décroissante sur , constante en 0 puis croissante sur non ?

[Sa Majesté]

Oui (sauf que "constante en 0", ça ne veut rien dire).
Maintenant ce qui est intéressant c'est le signe de g.

[Seth]

Oupsi pardon, je ne referai plus l'erreur :facepalm:.

Négative en et positive en ? Pourquoi ?

[Sa Majesté]

Négative en ?

Euh ... non. Je parle du signe de g.
Tu as perdu le fil, reprends les posts précédents.

[Seth]

Tout le temps positive (my bad).

[Sa Majesté]

Oui et donc ?
Bon je te laisse, je pars au boulot !

[Seth]

Attends attends... Comme elle est positive sur donc la suite est croissante ?

[Seth]

D'accord, merci beaucoup pour ton aide en tout cas !