Etude de SLn(R) - Sous-variété et connexité

[wartenberg]

Bonjour,

Je me posais la question suivante : une sous-variété (différentiable) est-elle nécessairement connexe ?
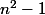
En d'autres termes, le fait d'avoir prouvé que est une sous-variété (de dimension ) de permet-elle d'affirmer que est connexe ?
Sinon, y-a-t-il un moyen simple de voir cela ?

Merci d'avance pour votre aide !

[infernaleur]

Salut,
Non, par exemple les ouverts de R sont des sous variétés de R, donc un truc de la forme ]0,2[\{1} est une sous variété de R qui n’est pas connexe.

(Après je suis entrain d’étudier la géo diff donc je sais pas si il existe des propriétés de connexité, mais je pense qu’elles doivent être locales.)

[GaBuZoMeu]

Ou encore, pour rester dans le registre des groupes linéaires, n'est pas connexe, bien que ce soit une sous-variété de (puisque c'en est un ouvert).

[wartenberg]

Ok, merci. C'est donc bien ce qu'il me semblait, (je voulais juste éviter de prouver "deux fois la même chose !).