Etude de raccords équa diff 1er ordre

[Ben314]

A mon avis, tu peut peut quand même être "pas mal" plus efficace dans la rédaction :



(1)
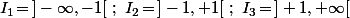
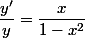
Et, sur chacun des 3 intervalles donne puis, aprés calculs

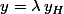
(2) v.d.c. On se place sur un des 3 intervalles et on pose où est une fonction :



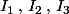
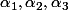
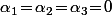
(3) Recollement : La formule çi dessus est valable sur chacun des intervalles mais bien entendu avec trois constantes quelconques et sans rapport les unes avec les autres. Mais si on veut une solution définie et continue sur , il faut que sur chaque intervalle la fonction admette une limite en -1 et/ou en 1 ce qui impose clairement . L'unique solution potentielle sur est donc qui est bien évidement dérivable et même sur et comme elle vérifie (E) sur privé de 1 et -1, par continuité, elle vérifie en fait (E) sur tout entier. (l'argument ici réside dans le fait que, vu que est , la fonction est continue donc, comme elle est identiquement nulle pour voisin de +1 et de -1, c'est qu'elle est aussi nulle pour x=+1 et x=-1: argument qui évite toute forme de vérification calculatoire)

[Gurvan44]

ok merci beaucoup pour ta réponse très complète et très claire ! Je sens qu'il faut simplement que je m’entraîne afin de prendre un certain recul