étude de limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 13:46
par ptitmatteo » 07 Nov 2007, 13:46
mais
(3/2)/(3x) n'est pas égale a 1/2x
???
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 13:51
par ptitmatteo » 07 Nov 2007, 13:51
[quote="ptitmatteo"]donc j'essayer de faire
on voit que:
sin(3x)/2x=(3/2).sin(3x)/3x
on fait un changement de variable on pose u=3x
donc sa devient
lim u.sin(u)/u = 1 . 3/2 = 3/2
u->0
QUOTE]
es que c'est mieu??
mais comment tu faitpour arriver a cette formule???
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 14:05
par ptitmatteo » 07 Nov 2007, 14:05
SimonB a écrit:Pour la dernière, écris
}{sin(5x)}=\frac{sin(2x)}{2x}\frac{5x}{sin(5x)}\frac{2}{5})
mais comment tu fait pour avoir cela??
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 14:31
par ptitmatteo » 07 Nov 2007, 14:31
personne peut m'expliquer???
-
SimonB
 par SimonB » 07 Nov 2007, 14:35
par SimonB » 07 Nov 2007, 14:35
ptitmatteo a écrit:mais comment tu fait pour avoir cela??
Tu connais les trucs de la forme sin(u)/u (tu connais leur limite quand u tend vers 0 en tous cas).
Donc tu essayes de tout rapporter à du sin(u)/u. Ici, j'ai simplement écrit que sin(u)/sin(v)=(sin(u)/u)*(sin(v)/v)*(v/u), ce qui est toujours vrai. Là, comme u et v sont deux trucs linéaires en x, ça se passe bien.
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 14:47
par ptitmatteo » 07 Nov 2007, 14:47
ah oui
mai la il faut que je divive ma limite en trois
lim
}{2x})
x-->0
on fait comme taleur donc sa fait 1
lim

x-->0
puis
lim 5x/sin(5x)
x-->0
mais je pense savoir mais je ne sais pas si on a le droit
moi j'aurais fait
}= [\frac{sin(5x)}{5x})
]^-1
mais après es qu'on peut utiliser la formule ave u
-
SimonB
 par SimonB » 07 Nov 2007, 14:51
par SimonB » 07 Nov 2007, 14:51
Oui, si la limite d'un truc est non nulle, la limite de l'inverse du truc est l'inverse de la limite du truc.
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 15:05
par ptitmatteo » 07 Nov 2007, 15:05
ok donc sa me fait
on sais que:
}{sin(5X)})
=
}{2x})
.
})
.
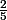
on pose u=2x
lim
}{u})
= 1
u-->0
on peut que
})
=[
}{5x})
]^-1
on pose v= 5x
lim [
}{v})
]^-1 = 1
v-->0
et on sais que 1=1^-1
donc
lim
}{2x})
.
})
.
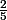
=
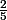
x-->0
es que c'est bon ??
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 15:20
par ptitmatteo » 07 Nov 2007, 15:20
et pour la derniere
il me dise de montrer que
lim
}{x^2})
=1
x-->0
mais je ne sais pas quoi faire
????
j'ai mis deux en facteur sa me fait
}{x^2})
mais après je ne sais pas quoi faire
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 15:29
par ptitmatteo » 07 Nov 2007, 15:29
personne que venir a mon aide??
-
SimonB
 par SimonB » 07 Nov 2007, 15:42
par SimonB » 07 Nov 2007, 15:42
Connais-tu la notion de développement limité ?
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 15:47
par ptitmatteo » 07 Nov 2007, 15:47
du tout car le prof a dit qu'il falait prendre des theoreme que l'on connait
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 15:52
par ptitmatteo » 07 Nov 2007, 15:52
sa consiste en quoi
 par legeniedesalpages » 07 Nov 2007, 15:59
par legeniedesalpages » 07 Nov 2007, 15:59
Bonjour, sans passer par les DL,
}{x^2} \\<br />= \frac{2(1-\cos(x))}{x^2} \\<br />= \frac{2(1-\cos(x))(1+\cos(x))}{x^2(1+\cos(x))} \\<br />= \frac{2(1-\cos^2(x))}{x^2(1+\cos(x))} \\<br />= \frac{2\sin^2(x)}{x^2(1+\cos(x))} \\<br />= \frac{2}{1+\cos(x)} (\frac{\sin(x)}{x})^2)
.
Je te laisse finir.
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 16:34
par ptitmatteo » 07 Nov 2007, 16:34
} (\frac{\sin(x)}{x})^2)
es que je peut l'étudier en 2
d'un coter
})
en disent que sa c'est égale
}{2})
]^-1
puis de faire un encadrement de cos(x)
-10
puis
lim

= 0
x-->0
donc
lim
}{x})
= 0
x-->0
es que es juste
 par legeniedesalpages » 07 Nov 2007, 16:46
par legeniedesalpages » 07 Nov 2007, 16:46
tu te compliques la vie.
Tu utilises comme tu dis les résultats de ton cours.
 \rightarrow 1)
quand

,
donc
 \rightarrow 2)
quand

,
donc
} \rightarrow \frac{2}{2}=1)
quand
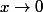
.
Dans ton cours on a du te donner la limite remarquable :

quand
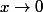
Donc
^2 \rightarrow 1^2=1)
quand
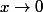
.
par conséquent:
} (\frac{\sin x}{x})^2 \rightarrow 1\times 1 = 1)
quand

.
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 16:57
par ptitmatteo » 07 Nov 2007, 16:57
mais comment tu sais que
lim cos(x)=1
x-->0
???
 par legeniedesalpages » 07 Nov 2007, 17:03
par legeniedesalpages » 07 Nov 2007, 17:03
)
est continue sur

(il me semble que c'est admis, me rappelle pas avoir vu un cours où on le montre, mais ça doit se faire à l'aide de la définition du cosinus avec le cercle trigonométrique,

)
ceci veut dire que pour tout
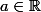
,
 = \cos(a))
.
En particulier pour

(en se rappelant que
=1)
).
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 07 Nov 2007, 17:07
par ptitmatteo » 07 Nov 2007, 17:07
et pareil pour
}{x})
pour c'est égale a 1
 par legeniedesalpages » 07 Nov 2007, 17:10
par legeniedesalpages » 07 Nov 2007, 17:10
ça c'est plus compliqué.
ça doit être un résultat de ton cours. En général elle est donnée en premiere.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
