Etude limite intégrale.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 24 Jan 2012, 20:16
par Deluxor » 24 Jan 2012, 20:16
Bonsoir.
Pouvez vous me guider dans la résolution de cet exercice?
On veut étudier en fonction des valeurs de

si la limite suivante est finie ou infinie :
^{\beta}}\, \mathrm dt \qquad (2))
On notera :
 \, = \, \frac{1}{t^{\alpha}(lnt)^{\beta}})
1. On suppose que

. On pose
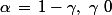
. Montrer que :
 \, \geq \, C \frac{1}{t^{1-\frac{\gamma}{2}}}, \, t \, \geq \, 2)
.
La limite
)
est-elle finie dans ce cas?
2. On suppose que

. On pose

. Montrer que :
 \, \leq \, C \frac{1}{t^{1+\frac{\gamma}{2}}}, \, t \, \geq \, 2)
.
La limite
)
est-elle finie dans ce cas?
3. Dans le cas
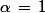
, discuter la finitude de la limite
)
en fonction des valeurs de

.
Merci d'avance.

-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 24 Jan 2012, 20:37
par Le_chat » 24 Jan 2012, 20:37
Salut. Tu en es où?
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 27 Jan 2012, 18:27
par Deluxor » 27 Jan 2012, 18:27
Salut
Le_chat !
Je bloque déjà à la première question.
 \, = \, \frac{1}{t^{1-\gamma} \, (lnt)^{\beta}})
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 27 Jan 2012, 18:51
par Le_chat » 27 Jan 2012, 18:51
t'as regardé ce que ça faisait f*t^(1-gamma/2)?
Parce que en fait on veut juste montrer que ce truc va pas trop s'approcher de 0.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 29 Jan 2012, 10:38
par Deluxor » 29 Jan 2012, 10:38
Le_chat a écrit:t'as regardé ce que ça faisait f*t^(1-gamma/2)?
Parce que en fait on veut juste montrer que ce truc va pas trop s'approcher de 0.
Je trouve que
^{\beta}})
, non?
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 29 Jan 2012, 13:30
par Le_chat » 29 Jan 2012, 13:30
non tu t'es planté, refais bien le calcul.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 02 Fév 2012, 15:59
par Deluxor » 02 Fév 2012, 15:59
J'en suis à :
 = \frac{1}{t^{1-\frac{\gamma}{2}}} . \frac{t^{\frac{\gamma}{2}}}{(lnt)^{\beta}})
avec
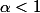
.
Comment poursuivre? Comment en déduire que :
 \, \geq \, C . \frac{1}{t^{1-\frac{\gamma}{2}}})
?
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 02 Fév 2012, 21:53
par Deluxor » 02 Fév 2012, 21:53
Personne? :cry:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités