Etude de fonction polynomiale.

[Deluxor]

Bonsoir,



1) J'ai montré que : et .

2) J'ai montré que P_n est strictement croissante sur [0; + \infty [.

Il me faut en déduire que, pour tout , il existe un unique réel strictement positif tel que : .

J'ai dit que est définie, continue et monotone sur . Comment faire pour montrer que 0 est dans l'intervalle d'arrivée ? et . Est-ce juste ?

Préciser et . S'agit-il bien des deux valeurs de x trouvées dans la question précédente ?

3) a. Comparer et
b. En déduire que la suite est décroissante, puis convergente. On note sa limite.

4) a. Montrer que : \forall n \geq 2, 0 \lt x_n \leq \frac{3}{4}
b. En déduire que :

5) a. Vérifier que :
b. En déduire que :
c. Déterminer alors


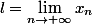
Merci d'avance!

[Nightmare]

Bonsoir,

tu es sûr que Pn(1)=0 ? Si c'était le cas, la question 2)bis n'aurait aucun intérêt, tu n'es pas d'accord?

[Deluxor]

plutôt, non?

[Nightmare]

Non plus, essaye de calculer P1(1), P2(1), P3(1)...

Qui plus est, pourquoi, machinalement, as-tu calculé la valeur en 1? A priori, si on demande de montrer que ça s'annule sur [0;+oo[, le reflex est de calculer la limite en +oo (comme tu l'as fait) et en 0, pas en 1...

Je ne vois pas pourquoi tu as fait ce choix de calculer la valeur en 1.

[Deluxor]

Non plus, essaye de calculer P1(1), P2(1), P3(1)...

Qui plus est, pourquoi, machinalement, as-tu calculé la valeur en 1? A priori, si on demande de montrer que ça s'annule sur [0;+oo[, le reflex est de calculer la limite en +oo (comme tu l'as fait) et en 0, pas en 1...

Je ne vois pas pourquoi tu as fait ce choix de calculer la valeur en 1.

C'est justement ce que je viens de me dire, et que je postais.

Et donc : ?

[Nightmare]

Ah, là, nous sommes d'accord !

Donc en résumé :

1) Pn(0) est négatif
2) Pn(+oo) est positif
3) Pn est strictement croissante

donc...

[Deluxor]

Ah, là, nous sommes d'accord !

Donc en résumé :

1) Pn(0) est négatif
2) Pn(+oo) est positif
3) Pn est strictement croissante

donc...

Merci!
J'ai utilisé le théorème de bijection.
Est-ce que mes et sont justes (solutions de la question 1) ?

[Nightmare]

Oui, ta réponse pour x1 et x2 est bonne!

[Deluxor]

Dac !

Je ne vois pas exactement à quoi correspondent et .

Est-ce juste de dire que ?

[Nightmare]

?

D'où ça vient ça?

Que vaut, en utilisant la définition de Pn(x), ?

[Deluxor]

[Nightmare]

Ok, peut être qu'en l'écrivant sans le signe somme, tu auras plus de facilité à comprendre le résultat vers lequel je t'amène.

Maintenant, on sait que , qu'est-ce que cela veut dire, toujours en utilisant la définition de Pn ? (Et toujours en évitant l'emploie du symbole somme)

[Deluxor]

On a donc : ?

Maintenant : . Comment simplifier? Je ne vois pas bien.

[Nightmare]

Hello,

C'est ok pour P(n+1)(xn).

Pour P(n+1)(x(n+1)) Rappelle moi quelle est la définition de x(n+1)?

Es-tu d'ailleurs sûr de l'énoncé?

[Deluxor]

Salut!

Sûr de l'énoncé? L'expression de est exacte, oui.

est la valeur de x pour laquelle ?

[Nightmare]

Oui, donc P(n+1)(x(n+1))=0, et je ne vois pas trop du coup ce qu'on attend comme "comparaison" entre 0 et P(n+1)(xn) ...

[Deluxor]

Oui, il aurait en fait fallu arriver à pour ensuite montrer que la suite est décroissante, non?

[Nightmare]

J'ai fini par comprendre ce qu'attendait de nous l'énoncé.

et . Par définition, x(n) est positif, donc

A partir de là, comment conclure que ?

[Deluxor]

Par la croissance de !

[Nightmare]

Yep c'est bien ça!