étude de convergence de suites

[MacManus]

Bonjour

J'aimerais avoir un avis et un peu d'aide sur l'exercice suivant :

1/
soit la suite de terme général
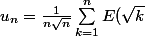(E est la fonction partie entière)
est divergente...

2/
soit la suite de terme général

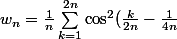je n'arrive pas à simplifier le terme général pour trouver la limite si elle existe...

Merci à vous!

[Nightmare]

Salut :happy3:

Pour la 2ème; as-tu essayé de linéariser puis de faire un DL?

[MacManus]

pour la linéarisation de , je trouve ceci :



c'est correct ??

[leon1789]

pour la linéarisation de , je trouve ceci :



c'est correct ??

Ton résultat ne dépend pas de k, étrange non ?

[Doraki]

La première suite est divergente, vraiment ?
Tu connais les intégrales de Riemann ? (t'as intérêt)

Pour le 1/ tu peux étudier la suite sans la partie entière à la place si tu montres que la différence entre la suite et la suite sans partie entière tend vers 0.

Après, quand tu as fait ça tu n'as plus qu'à dessiner des petits rectangles sous certaines portions de courbes, comme y = sqrt(x) pour la 1 et y = cos²(x) pour la 2.

[MacManus]

oui on obtient plutôt non ??

[leon1789]

oui on obtient plutôt non ??

oui :we: :we:

[MacManus]

ok merci et comment faire ensuite pour le DL ? je connais le DL de cos(x) au voisinage de 0 , mais je ne vois pas comment l'introduire dans l'expression de ...

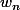
[Nightmare]

En fait on a même pas besoin de DL, tu développes ton cosinus avec les formules d'addition puis tu fais apparaitre une somme de Riemann.

:happy3:

[MacManus]

j'obtiens
mais je suis un peu bloqué...

[Nightmare]

Ben il ne te reste plus qu'à développer et tes sommes de Riemann apparaissent (attention, on va intégrer sur [0,2])

[MacManus]

désolé pour le temps de réponse mon ordi est lent...
peux-tu m'éclairer un peu plus car je n'arrive pas à voir mes sommes de Riemann pourquoi on intègre sur [0,2] d'ailleurs?)
merci pour ton aide!

[Nightmare]

Par exemple le premier terme :

, c'est une jolie somme de Riemann non?

[MacManus]

d'accord on a : +

mais tu ne sommes plus de 1 à 2n mais de 0 à 2n en changeant l'expression du cosinus et du sinus, ca revient au même alors ?

[Doraki]

C'est moins compliqué de faire une somme de Riemann avec l'expression de départ nan ?

[Nightmare]

Tu ne peux pas à cause du -1/(4n)

[Doraki]

Justement c'est mieux parceque la valeur qu'on prend pour la hauteur du rectangle posé sur l'intervalle [(2k-2)/4n ; 2k/4n] c'est la valeur de f en (2k-1)/4n, soit au milieu.

[leon1789]

C'est moins compliqué de faire une somme de Riemann avec l'expression de départ nan ?

Tu ne peux pas à cause du -1/(4n)

Comme Doraki, je crois que

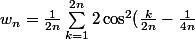est l'approximation de par la méthode du point médian avec un découpage en 2n sous-intervalles.

[Nightmare]

Effectivement, mais faut aller le chercher!

[MacManus]

merci à vous j'ai compris votre raisonnement. j'avoue que tout ça m'étais sorti un peu de la tête! merci encore