A+b = 75 est ce qu'on peut trouver a-b/ab ?

[savan-306D]

Salut et bonsoir,
Etant donné la somme de deux nombres a+b = 75
calculer (a-b)/ab
et merci d'avance.

[Black Jack]

est-ce qu'on peut calculer leur difference ou leur produit ?

Non.

Il vaudrait mieux donner un énoncé correct et complet.

:zen:

[jlb]

Salut et bonsoir,
Je suis tombé sur un exos de physique, ou on a deux inconnus a,b
on a leur somme a+b = 75
est-ce qu'on peut calculer leur difference ou leur produit ?
a+b = 75 trouvez a-b/ab
et merci d'avance.

ben non prends par exemple a=74 et b=1 puis a=73 et b=2, tu trouves des valeurs différentes pour ton expression

[Losange]

Testez sur quelques exemples. Vous verrez qu'on peut trouver des valeurs très différentes pour (a-b)/ab.

[LA solution]

Testez sur quelques exemples. Vous verrez qu'on peut trouver des valeurs très différentes pour (a-b)/ab.

mon cher on es dans quel ensemble ?

[deltab]

Bonjour.

La connaissance de la somme s=a+b permet effectivement de connaitre a-b et ab mais ces 2 expressions seront des expressions avec paramètres (on pourra choisir a ou b comme paramètre).



et

Pour on aura et

Le rapport lui n'est pas toujours défini, cas où ou

[ahlilioune]

a + b = 75
on a par exemple a = 50 et b = 25

a - b = 25 et a.b = 1250

donc 25|1250 est vraie 1250 = 25 . 50
a| b b = a . k

[deltab]

Bonsoir

a + b = 75
on a par exemple a = 50 et b = 25

a - b = 25 et a.b = 1250

donc 25|1250 est vraie 1250 = 25 . 50
a| b b = a . k

Le problème posé est apparemment le suivant: trouver les entiers naturels et tels que 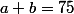et 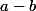divise .
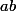Si c'est le cas, le nombre de solution de a+b=75 dans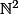 est fini (76 solutions en tout), on peut alors toutes les tester pour la deuxième condition. En tenant compte que si est une solution du problème, l'est aussi, il suffit de tester les solutions vérifiant 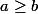qui sont au nombre de 38.

a=75 ==> b=0, a-b=75, ab=0 75 divise 0, 0x (-75)=0
a=74 ==> b=1, a-b=73, ab=74 73 ne divise pas 74
a=72 ==> b=3, a-b=69, ab=216 69 ne divise pas 216
...
a=70 ==> b= 5, a-b=65, ab=350 65 ne divise pas 350 ,65x5=325, 65x6=385
...
a=60 ==> b=15, a-b=45, ab=1400 45 ne divise pas 1400
....
a=65 ==> b=10, a-b=55, ab=650 55 ne divise pas 650
---
a=55 ==> b=20, a-b=30, ab=1100 30 ne divise pas 1100
---
a=50 ==> b=25, a-b=25, ab=1250 25 divise 125
---