B(X,Y) est complet
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 09:35
par Pythix » 15 Sep 2007, 09:35
Bonjour,
je cherche à montrer que l'ensemble des fonctions bornées B(X,Y) muni de la distance uniforme est complet, sachant que Y est complet.
j'ai pris une suite de cauchy
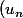\in B(X,Y))
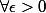


-u_{q}(x)|<\epsilon)
d'ou
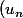)
est de cauchy dans Y, donc converge vers une limite l...
et là je vois plus trop ce que je dois faire...
Merci d'avance
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 15 Sep 2007, 09:39
par yos » 15 Sep 2007, 09:39
Pythix a écrit:d'ou
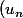)
est de cauchy dans Y, donc converge vers une limite l...
C'est plutôt :
pour chaque

de

,
))
est de Cauchy dans Y complet donc converge vers une limite
)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 09:41
par fahr451 » 15 Sep 2007, 09:41
bonjour
attention à ce que tu écris
u n de cauchy dans B c 'est l 'hypothèse
qu elle converge c 'est ce que tu veuxmontrer ....
pour x fixé dans X
u n ( x) est de cauchy dans Y
car ll un (x) - up(x) ll =< sup ll ll ( pour moi ce sont des ll ll et non des l l)
or Y complet donc un(x) converge vers un certain u(x) dans Y
reste à finir
u bornée? et un converge vers u pour la norme sup ? ( c est simple)
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 15 Sep 2007, 10:00
par Lierre Aeripz » 15 Sep 2007, 10:00
Voici le plan classique d'une démonstration de complétude :
- On prend une suite de Cauchy
- On construit ce qui sera la limite
- On montre que l'objet construit est bien dans l'ensemble étudié
- On montre que la suite converge bien vers cette limite (NB : ceci suffit à prouver le 3ème point si l'on sait que l'ensemble est fermé.)
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 10:18
par Pythix » 15 Sep 2007, 10:18
oui j'ai pas relu ce que j'ai tapé, c'est bien u_n(x) qui converge vers l(x).
il me reste donc à montrer que u_n converge (uniformément ou simplement?) vers l(x) et que l(x) est bien dans B(X,Y) ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 10:23
par fahr451 » 15 Sep 2007, 10:23
u doit converger vers l uniformément bien sûr
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 10:29
par Pythix » 15 Sep 2007, 10:29
c'est ce qui parait s'imposer oui, par contre je vois pas bien pourquoi?
pour conclure que u_n converge vers l ?
Pour dire que la convergence se fait dans l'ensemble ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 10:38
par fahr451 » 15 Sep 2007, 10:38
pour epsilon
il existe N tels que pour
n,p> N et pour tout x
ll un(x) -up(x) ll < epsilon
n fixé p ->+infini on obtient
n>N pour tout x ll un(x) -l(x) ll =< epsilon
soit
sup ll un (x) -l(x)ll =< epsilon
et exactement la cv uniforme de un - l vers 0
puis sup ll l (x) ll =< sup ll un(x) ll +epsilon assure que l est borné
et l'inégalité précédente dit exactement u converge vers l au sens de la norme infinie
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 10:46
par Pythix » 15 Sep 2007, 10:46
merci !
dernière question, peut on dire que si X est compact
comme C(X,Y) incluse dans X alors cette dernière est incluse et fermée dans B(X,Y) ?
et donc C(X,Y) est complet?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 10:51
par fahr451 » 15 Sep 2007, 10:51
je ne comprends pas C(X,Y) incluse dans X
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 10:57
par Pythix » 15 Sep 2007, 10:57
C(X,Y) est l'ensemble des fonctions continues de X
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 10:57
par fahr451 » 15 Sep 2007, 10:57
c est inclus dans X ??
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 11:08
par Pythix » 15 Sep 2007, 11:08
euh... ben la question est :
on suppose désormais que X est compact. Montrer que C(X,Y) est inclus dans B(X,Y) et que C(X,Y) est une partie fermée de B(X,Y).
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 11:18
par Pythix » 15 Sep 2007, 11:18
ben si c'est pas inclus dans X comment ca pourrait l'etre dans B(X,Y) ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 15 Sep 2007, 12:41
par yos » 15 Sep 2007, 12:41
Allo Houston, on a un problème.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 12:43
par fahr451 » 15 Sep 2007, 12:43
rogers rogers l'appareil n'est plus sous contrôle
meday meday il faut penser à s 'éjecter
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 15 Sep 2007, 12:57
par yos » 15 Sep 2007, 12:57
X est l'ensemble de départ des fonctions qui appartiennent à B(X,Y) ou à
C(X,Y) donc il n'y a pas de relation d'inclusion entre les deux.
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 15:34
par Pythix » 15 Sep 2007, 15:34
oula, j'ai honte....
donc on peut dire que f en tant qu'application continue sur un compact est bornée,
et après pour montrer que C(X,Y) est fermé je vois pas trop... peut etre avec l'uniforme continuité (Heine) ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 15:49
par fahr451 » 15 Sep 2007, 15:49
une limite uniforme de fonctions continue est continue ce qui assûre le caractère de C°
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 15 Sep 2007, 16:56
par Pythix » 15 Sep 2007, 16:56
je n'ai pas vu cette propriété en cours
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités