Espaces vectoriels

[sup BCPST]

Bonjour,

Je suis en sup BCPST et j'ai un devoir à faire sur les éspaces vectoriels et j'avoue que je trouve ce chapitre pas évident du tout se qui me pousse à vous demander un peu d'aide pour les premières questions histoire de me débloquer.

Alors, voici le début de l'énoncé:

On désigne par E l'ensemble des applications de R(l'ensemble des réels) dans R, deux fois dérivales sur R et par F le sous-ensemble de E des applications f telles que: f"-3f'+2f=0

On désigne par F° le sous-ensemble de F des applications f telles que:
f(0)=f'(0)=0

1- Montrer que E est un espace vectoriel réel. Montrer que f et f° sont des sous-espaces vectoriels de E.

2- Soit f un élément de F
Montrer qu'il existe un unique couple (a1,a2) de réels tel que f-a1f1-a2f2 appartienne à F°.


Merci beaucoup pour votre aide.

[Zebulon]

Bonsoir,
pour la première question, il s'agit seulement de vérifier les axiomes des espaces vectoriels. Tu dois avoir vu que la définition d'un espace vectoriel E sur un corps K (ici ) est un ensemble qui vérifie un certain nombre de lois. Il suffit donc de vérifier que E les satisfait. Idem pour les sous-espaces vectoriels.
Pour la deuxième question, qui sont et ?
En espérant pouvoir t'apporter mon aide,
Zeb.

[sup BCPST]

Bonsoir,

Oui effectivement je sais que un espace vectoriel doit être commutatif, associatif, admettre un élément neutre, un sysmétrique... mais c'est que j'arrivais pas à le faire de façon rigoureuse, en fait j'ai du mal à manipuler les applications.

Sinon, excuse moi j'avais pris la deuxième question un peu plus bas dans mon énoncé et j'ai oublié de préciser f1 et f2.

f1(x)=e^x
f2(x)=e^(2x)

Voilà, voilà, j'espère que tu arriveras à m'aider pour cette question.
merci

[Zebulon]

Bonjour,
pour la deuxième question, je te suggère de regarder les conditions nécessaires sur et :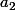
soit , supposons:
tels que
(1) .
(1) est vrai si et seulement si (1'): et (1''):.
Tu supposes donc qu'il existe tels que (1) et tu montres qu'alors (1') est vrai.
Ensuite tu supposes toujours qu'il existe ,et cette fois tels que (1'') est vrai. Alors tu déduis les valeurs de et 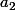, dans le cas où elles existent bien sûr. A toi de voir si elles peuvent bien exister ou non... (oui, bien sûr qu'elles existent car on arrive à les définir, et on prouve de plus leur unicité).
Après ça, pour montrer leur existence, tu poses et 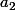=leur valeur nécessaire que tu as trouvées précédemment et tu montres que ce sont des conditions suffisantes à (1) et... le tour est joué!!! :we:
Bon courage et à bientôt,
Zeb.