Espaces vectoriels

[manianga]

bonjour tout le monde j'ai un souci avec cet exercice

je dois prouver que l'ensemble S des (x,y,z) de R^3 tels que x^2+2y^2+2z^2+2xy+2zx=0 est un sous espace vectoriel de R^3
j'ai donc d'abord montrer que (0,0,0) appartient a s
puis ensuite j'ai poser f(x,y,z)=x^2+2y^2+2z^2+2xy+2zx=0
puis si x1,y1,z1 est dans S alors f(x1,y1,z1)=0 et j'ai fait de meme pour x2,y2,z2
mais lorsque que je calcule f(x1+x2,y1+y2,z1+z2) je ne trouve pas 0
est ce une erreur de calcul ou de raisonnement?

merci de votre aide

[nuage]

Salut,
C'est sans doute une erreur de calcul.
La question a déjas été posé sur ce forum.
La méthode la plus simple (à mon avis) est de remarquer que :

[manianga]

oui j'ai aussi essayer par cette méthode mais la je ne comprend pas comment continuer il faut montrer les 3 propriétés que 0 appartiennent au sev puis l'addition et la multiplication mais la je ne comprend pas ce calcul

[nuage]

La somme des carrés de deux réels est nulle si et seulement si les deux nombres sont nuls.
La condition donnée est donc équivalente à : x+y+z=0 et x-y=0.
Il est facile de vérifier que (0;0;0) la verifie.
Si (a;b;c) la vérifie c'est aussi le cas pour k(a;b;c)
Si (a;b;c) et (a';b';c') verifie tous deux la condition on voit que :
(a+a')+(b+b')+(c+c')=( a+b+c)+(a'+b'+c')=0+0=0
et que (b+b')-(c+c')=(b-c)+(b'-c')=0.
Donc (a;b;c)+(a';b';c') vérifie aussi la condition.

L'avantage de la transformation est de simplifier les calculs (et de déterminer facilement le sous espace en question).
Mais on doit pouvoir montrer la même chose directement avec la condition telle q'elle est donnée dans l'ennoncé.

[Gato]

Les sous espaces vectoriels de étant parfaitement connus (vecteur nul , droites ,plans et espace tout entier) on en déduit que l'équation initiale va pouvoir ce ramener à une ou deux équations (droite ou plan).

Nuage t'a bien aidé ; je te donne une petite indication : si a et b sont deux réels ,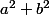 équivaut à .
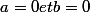L'intersection de deux sous espaces vectoriels est un sous espace vectoriel.